Quelques opérateurs gradient
Introduction
Ces opérateurs sont à considérer comme des filtres qui vont être corrélés à l'image. Les réponses impulsionnelles de ces filtres peuvent se présenter sous la forme de fonctions analytiques souvent d'une seule variable ou bien sous la forme de masques bi-dimensionnels. Dans les deux cas le filtrage a lieu en deux étapes : un filtrage suivant les lignes de l'image puis suivant les colonnes dans le cas d'une expression monodimensionnelle de la réponse impulsionnelle du filtre, une corrélation bi-dimensionnelle de l'image avec deux masques modélisant deux contours dans des directions orthogonales dans l'autre cas.
Opérateurs de gradient par masques
Introduction
Pour chaque opérateur, deux masques sont utilisés de façon à déterminer le gradient de l'image dans deux directions orthogonales.
Approximation de base
Le masque le plus intuitif à mettre en œuvre est un masque à deux éléments :
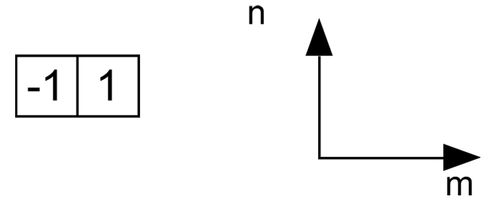
L'origine du masque est le point -1.
Dans le repère ci-dessus, la réponse impulsionnelle h(m,n) du masque est définie par :
h(0,0) = -1
h(1,0) = 1
La corrélation de ce masque avec une image de luminance f(i,j) s'écrit :
Il s'agit bien d'un calcul de gradient suivant l'axe horizontal. En faisant subir une rotation de
 au premier masque, il apparaît le filtre suivant dont l'origine est le point 1 :
au premier masque, il apparaît le filtre suivant dont l'origine est le point 1 :
La réponse impulsionnelle est telle que :
h(0,0) = 1
h(0,-1) = -1
La corrélation de ce masque avec l'image f(i,j) permet bien d'implanter un gradient dans la direction verticale :
La figure suivante propose une illustration de l'application de ces masques.
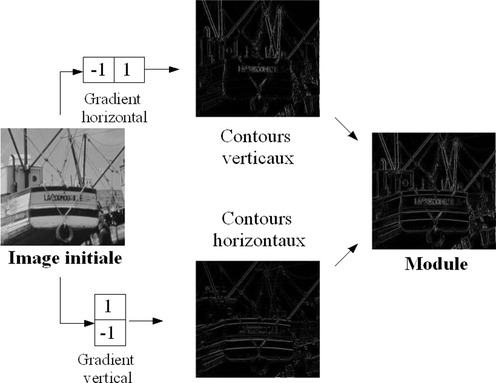
Opérateur de Roberts
Ce masque proposé en 1965 permet de calculer un gradient le long des diagonales de l'image :
L'origine est le point 1 tandis que la réponse impulsionnelle s'écrit :
h(0,0) = 1
h(-1,-1) = -1
La sortie obtenue après filtrage est :
Le deuxième masque se déduit du premier par rotation de
 :
:
L'origine est le point du haut à droite si bien que la réponse impulsionnelle est telle que :
h(-1,0) = 1
h(0,-1) = -1
La sortie obtenue après filtrage est :
La figure suivante propose une illustration de l'application de ces masques.
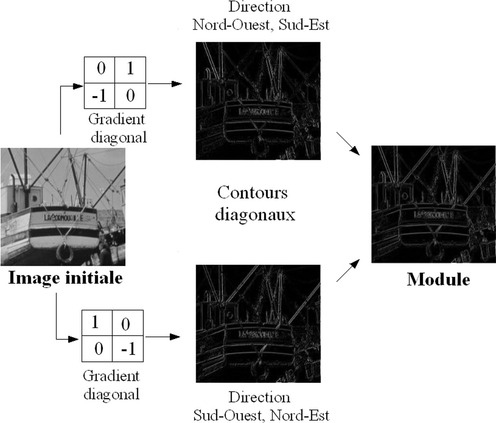
Le majeur inconvénient de ces masques réside dans leur forte sensibilité au bruit du fait de l'implantation de la dérivation qui se traduit par un filtrage passe-haut. D'autres masques ont ainsi été proposés afin de rendre le filtrage moins sensible au bruit.
Opérateurs de Prewitt et Sobel
Le calcul de gradient est mené par l'intermédiaire de deux masques, le premier effectuant un gradient horizontal, le second un gradient vertical. Là encore, le deuxième masque se déduit du premier par une rotation de
 . Les masques sont donnés ci-dessous pour les contours horizontaux puis verticaux.
. Les masques sont donnés ci-dessous pour les contours horizontaux puis verticaux.
Chaque pixel des masques est normalisé par
Lorsque c=1, il s'agit des opérateurs de Prewitt, lorsque c=2, de ceux de Sobel. Par rapport aux précedents, ces masques ont l'avantage de produire deux effets. Outre le calcul du gradient dans une direction, ces masques effectuent un lissage dans la direction orthogonale. Ce lissage rend ces masques un peu moins sensibles au bruit que les précédents.
L'origine de ces masques est toujours le pixel central. La réponse impulsionnelle h(m,n) des filtres de Prewitt et Sobel pour la mise en évidence des contours horizontaux est telle que :
h(-1,1) = h(1,1) = 1
h(-1,-1) = h(1,-1) = -1
h(0,1) = c
h(0,-1) = -c
La sortie obtenue après filtrage est :
L'équation laisse apparaître la double action avec un moyennage horizontal sur trois pixels sur les lignes au dessus et au dessous du pixel central et un calcul de gradient vertical entre les deux lignes.
Pour la mise en évidence des contours verticaux, c'est l'autre masque qui est utilisé. La sortie obtenue après filtrage peut se mettre sous la forme :
Cette écriture permet elle aussi de mettre en évidence la double action : un gradient horizontal est en effet calculé sur trois lignes puis un lissage vertical est opéré.
Les deux écritures employées montrent bien que les deux actions, lissage et dérivation, du filtrage de Prewitt ou de Sobel sont séparables.
La figure suivante propose une illustration de l'application des masques de Sobel.
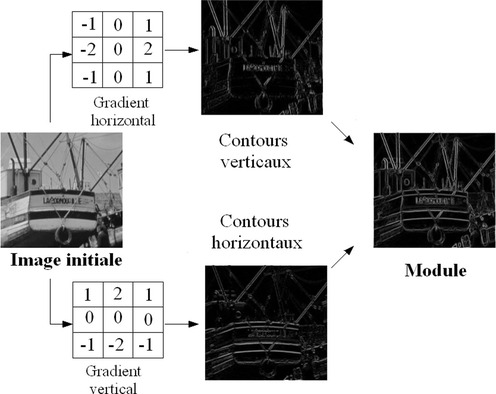
Il existe bien sûr beaucoup d'autres masques utilisés pour déterminer le gradient d'une image (Frei-Chen, ...). Le lecteur intéressé pourra consulter l'ouvrage [3] qui entreprend des études comparatives de plusieurs masques à partir d'images de test.
Le principal intérêt de ces masques est leur facilité de mise en œuvre ainsi que la rapidité de leur traitement. Leur inconvénient est leur grande sensibilité au bruit. De plus les contours obtenus sont souvent assez larges. D'après l'ouvrage [2], le filtre de Sobel est le plus utilisé dans les applications industrielles nécessitant des contraintes temps-réel.
Opérateur gradient boussole
Les opérateurs dits boussole mesurent le gradient dans des directions sélectionnées. L'image est successivement filtrée par un ensemble de masques mk(i,j) dont chacun représente une approximation discrète d'un contour idéal dans une orientation spécifique (voir figure ci-après). Le résultat du filtrage de l'image f(i,j) avec le kième masque est gk(i,j).
Il s'agit alors de garder les contours correspondant à l'orientation du masque ayant conduit au maximum des fonctions gk(i,j) avec k allant de 0 à 7, représentatif des huit principales directions d'une boussole. Un autre critère possible revient à chercher le masque correspondant à la direction du contour dont le coefficient de corrélation avec l'image initiale est le plus fort. Il s'agit de minimiser rk(i,j) l'inverse du coefficient de corrélation.
critère 1 :
critère 2 :
avec
Plusieurs masques peuvent être utilisés. La démarche consiste à choisir un type de masque puis à effectuer des permutations circulaires dans les huit directions possibles du gradient. Des exemples d'opérateurs gradient boussole dans la direction Nord sont présentés ci-dessous en recourant aux masques de Prewitt, de Kirsch, de Robinson de niveau 3 ou 5. Le terme de niveau désigne le nombre de valeurs différentes présentes dans le masque.
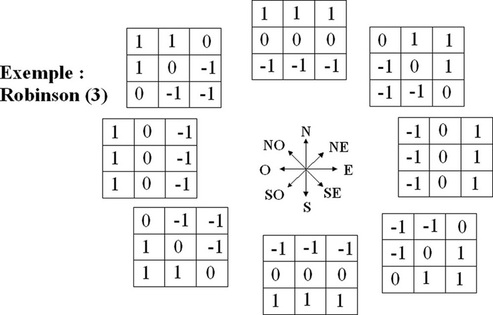
Filtrage de Canny
Principe
Les approches précédentes par masques étaient basées sur une modélisation assez simple d'un contour idéal. Pour le calcul du filtre de Canny, une approche analytique plus élaborée est employée. Il s'agit d'une technique de filtrage optimal. Canny a en effet cherché à déterminer de façon analytique en 1986 un filtre à partir de trois critères :
-
un critère de bonne détection garantissant une réponse forte en sortie du filtre même en présence de faibles contours sur l'image d'entrée,
-
un critère de bonne localisation du contour,
-
un critère d'unicité de la réponse permettant d'assurer une seule détection pour un contour et ainsi d'éviter les effets de rebond.
Canny définit ces trois critères de façon mathématique. L'optimisation des trois critères proposés permet de définir le filtre linéaire optimal pour la détection d'une marche d'escalier sous l'hypothèse d'un bruit additif indépendant du signal. Il s'agit de trouver la réponse impulsionnelle h(x) du filtre optimal qui permet d'obtenir une valeur maximum en sortie lorsqu'un contour est présenté en entrée. Canny souhaite un filtre à réponse impulsionnelle finie.
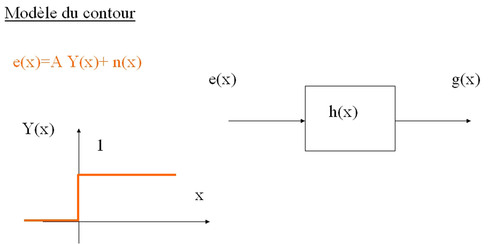
Le modèle de contour utilisé est une marche d'escalier :
où A représente l'amplitude du saut d'intensité, n(x) un bruit blanc additif indépendant de l'arête et Y(x) la fonction d'heaviside définie telle que :
La définition de l'arête est telle que le saut d'intensité se situe en x=0. Les hypothèses concernant le bruit additif sont :
où E[.] désigne l'espérance mathématique.
La moyenne des échantillons est nulle et les échantillons sont décorrélés. La sortie g(x) s'écrit comme la convolution de l'entrée e(x) par la réponse impulsionnelle du filtre recherché h(x) :
or
d'où
Le premier terme correspond au signal utile, le second au bruit. Du premier terme, on déduit :

Le filtre est donc un dérivateur.
Or pour mettre en évidence le contour, la sortie g(x) doit être maximale à l'endroit du contour, c'est-à-dire en x=0. Cette sortie sera donc paire et on en déduit que la réponse impulsionnelle h(x) du filtre optimal est impaire.
Critère de bonne décision
Le premier critère choisi par Canny est celui de bonne décision qui consiste à maximiser le rapport signal à bruit (RSB) en sortie du filtre même en cas de contour faible. Il est défini à l'endroit du contour en x=0 comme le rapport du maximum de la réponse due au signal sur la valeur efficace du bruit :
Canny obtient le critère suivant à maximiser (cf exercice « Critère de bonne décision ») :
avec
Critère de bonne localisation

En présence d'un contour noyé dans du bruit, il est probable que la sortie du filtre soit maximum en x=x0 et non pas en x=0. Soit X0 la variable aléatoire correspondant à la distance entre le maximum de la réponse g(x) et la position réelle de la transition (x=0). Le second critère à maximiser proposé par Canny est l'inverse de l'écart-type de la variable aléatoire X0 :
Canny cherche donc bien à minimiser la variance de l'écart entre la position du maximum en sortie de filtrage et la position réelle du contour. Le critère s'écrit finalement (cf exercice «Critère de bonne localisation»)
avec
Critère d'unicité de la réponse
Canny cherche à obtenir une faible multiplicité des maxima dus au bruit en décidant de maximiser la distance entre deux maxima de la sortie.

La distance à maximiser est donnée par x sur la sortie g(x), ce qui équivaut à 2 xmoy sur la sortie g'(x).
Le troisième critère s'écrit :
L'exercice «Critère d'unicité de la réponse » permet d'obtenir le critère à partir de l'illustration.
Obtention de la réponse impulsionnelle optimale
Le filtre est obtenu par optimisation des trois critères précédents : le premier Σ consiste à maximiser le rapport signal sur bruit et à garantir une réponse forte en sortie du filtre même en cas de contours faibles, le second Λ assure que les contours détectés par l'opérateur sont bien localisés sur les vrais contours, le troisième x vise à l'obtention d'une réponse unique pour un contour en évitant de multiples détections. Canny impose à la réponse impulsionnelle recherchée h(x) d'être à support borné sur l'intervalle [-w, w].
Le problème d'optimisation consiste à majorer le produit
 sous la contrainte x=kw avec :
sous la contrainte x=kw avec :
et
En considérant que h(x) est une fonction impaire :
le problème d'optimisation devient un problème de minimisation de
 sous les différentes contraintes :
sous les différentes contraintes :
Il s'agit alors de minimiser la fonctionnelle suivante :
où
 sont des multiplicateurs de Lagrange (réels).
sont des multiplicateurs de Lagrange (réels).
En utilisant l'équation d'Euler :
il vient :
L'équation différentielle résultante à résoudre est :

La solution de cette équation s'écrit pour
 :
:
L'extension de la réponse impulsionnelle sur l'intervalle [-w, w] se déduit aisément du fait du caractère impair du filtre.
Le détecteur de contour obtenu par Canny conduit à un produit
 sous la contrainte maximal x=kw . Les paramètres optimisés sont les suivants : α = 2,05, β = 2,92, ω =1,57, k = 0,58 , C=1 et x= 1,2. Les coefficients a1, a2, a3
et a4 de la réponse impulsionnelle h(x) sont des fonctions assez complexes de α, β et ω explicitées dans l'article [
] de Canny. A partir des paramètres donnés précédemment, on obtient les coefficients suivants : a1=-0,15, a2
=-0,21, a3=1,24 et a4=-0,79.
sous la contrainte maximal x=kw . Les paramètres optimisés sont les suivants : α = 2,05, β = 2,92, ω =1,57, k = 0,58 , C=1 et x= 1,2. Les coefficients a1, a2, a3
et a4 de la réponse impulsionnelle h(x) sont des fonctions assez complexes de α, β et ω explicitées dans l'article [
] de Canny. A partir des paramètres donnés précédemment, on obtient les coefficients suivants : a1=-0,15, a2
=-0,21, a3=1,24 et a4=-0,79.
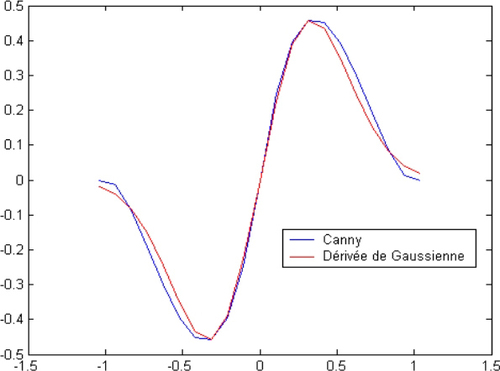
Pour faciliter la mise en oeuvre du détecteur de contour, Canny suggère le cas échéant de remplacer la réponse impulsionnelle optimale h(x) par celle de la dérivée d'une Gaussienne notée hG(x) :
En effet, la forme de la dérivée de Gaussienne s'approche assez bien de celle du filtre optimal pour une valeur du critère
 avec k = 0.51 et une performance moindre de 20 %.
avec k = 0.51 et une performance moindre de 20 %.
Interprétation
La détection de contour par calcul du gradient est sensible au bruit. Une idée avancée permettant d'atténuer ce problème consiste à filtrer passe-bas l'image avant d'appliquer l'opérateur Gradient. Mathématiquement cela revient à convoluer l'image initiale inchangée f(x,y) avec la dérivée de la réponse impulsionnelle h(x,y) du filtre passe-bas comme le montre l'écriture suivante dans le cas monodimensionnel :
Il reste à déterminer le filtre passe-bas pour h(x,y). Dans le cas d'un filtre gaussien, l'application du gradient consiste finalement à filtrer l'image initiale par une dérivée de Gaussienne hG(x) . C'est en fait à peu de chose près l'approche du filtrage de Canny.
Étapes d'une détection de contours par filtrage de Canny
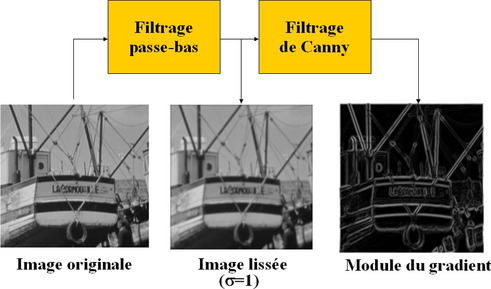
L'objectif est bien de calculer le module du gradient de l'image analysée. Souvent avant d'appliquer le filtre de Canny, un filtrage préalable est opéré sur l'image au moyen d'un filtre gaussien. Les différentes étapes sont énumérées ci-après :
-
convolution de l'image initiale avec un filtre passe-bas gaussien bi-dimensionnel (ou convolution 1D dans chacune des deux directions),
-
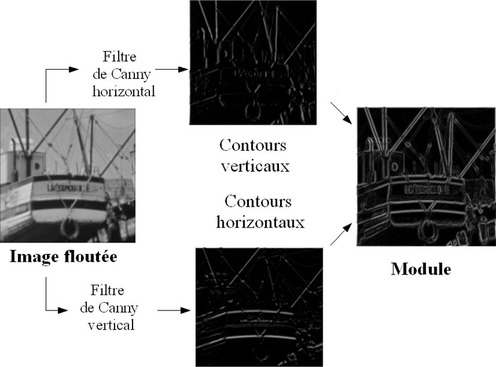
convolution de l'image lissée avec le filtre de Canny ou la dérivée de gaussienne dans les directions horizontale et verticale,
-
calcul du module du gradient à partir des deux images représentant les gradients de l'image filtrée passe-bas dans les directions horizontale et verticale.