Bandes d'énergie

Considérons un atome de silicium Si isolé, les niveaux énergétiques de ses électrons sont discrets (voir le modèle de Bohr pour l'hydrogène). Lorsque l'on rapproche de ce dernier un atome identique, les niveaux énergétiques discrets de ses électrons se scindent en deux sous l'interaction réciproque des deux atomes. Plus généralement, lorsque l'on approche N atomes, les niveaux énergétiques se scindent en N niveaux. Ces N niveaux sont très proches les uns des autres et si la valeur de N est grande, ce qui le cas pour un cristal, ils forment une bande d'énergie continue. La notion de rapprochement des atomes est donnée par la distance inter-atomique d.

A présent considérons des atomes de silicium Si arrangés aux nœuds d'un réseau périodique, mais avec une maille très grande de telle manière que les atomes puissent être considérés comme isolés. Les deux niveaux les plus énergétiques sont repérés par E1 et E2. Rapprochons homothétiquement les atomes les uns des autres, les états énergétique électronique se scindent et forment deux bandes continues appelées bande de conduction BC et bande de valence BV. La figure 1 montre la formation de ces bandes en fonction de la distance interatomique.

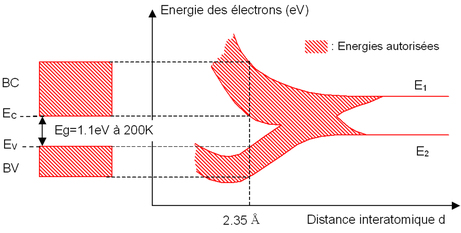
Pour les électrons d'un cristal de silicium ( 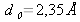), on constate qu'il existe deux bandes continues d'énergie (BC et BV) et que ces bandes sont séparées par une bande interdite car d'énergie inaccessible aux électrons. Cette région interdite est appelée « gap » et sa largeur Eg est caractéristique du matériau. Notons que l'énergie du bas de la bande de conduction est notée EC et que celle du haut de la bande valence est notée EV ainsi nous avons l'égalité Eg=EC-EV. Précisons que les bandes continues d'énergie BC et BV ne sont qu'une représentation des énergies accessibles par les électrons, ceci ne présage en rien de l'occupation effective de ces bandes par ces derniers.