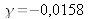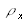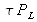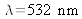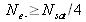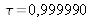Exercice : éclairage laser pulsé
Pour définir un capteur interférométrique, on s'intéresse au bilan photométrique du système d'éclairage de l'objet et de capture d'image.
L'objet d'intérêt est en acier d'albédo
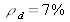 et de diamètre
et de diamètre
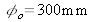 . L'objectif d'imagerie a une focale f' = 18 mm, une transmission Topt = 90% et possède une bague d'ouverture avec les nombres d'ouverture No = {2,8 ;4 ;5,6 ;8 ;11,3 ;16 ;22,6 ;32}. Pour des raisons de disposition l'objet sera éclairé avec une incidence moyenne
. L'objectif d'imagerie a une focale f' = 18 mm, une transmission Topt = 90% et possède une bague d'ouverture avec les nombres d'ouverture No = {2,8 ;4 ;5,6 ;8 ;11,3 ;16 ;22,6 ;32}. Pour des raisons de disposition l'objet sera éclairé avec une incidence moyenne
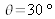 .
.
Le capteur CCD utilisé possède MxN = 1024´1360 pixels de taille px = py = 4,65 mm, chaque pixel contient Nsat = 18000 électrons à la saturation et la fréquence pixel est de 20 MHz. Le temps d'intégration peut être réglé entre 5 ms et 65 s.
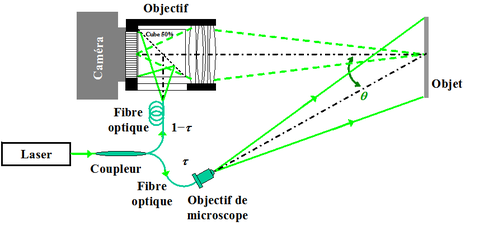
On utilise un laser NdYAG pulsé et doublé avec un cristal de KDP, les impulsions délivrées ayant une durée de 20 ns. Le laser peut être cadencé entre 30 et 60 Hz. Le dispositif expérimental d'imagerie laser est décrit Figure 2. Un coupleur à transmission variable (non détaillé ici) permet de séparer l'onde laser en une partie « éclairage objet » (transmission
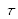 ) et une partie « référence » qui vient directement éclairer le capteur (transmission
) et une partie « référence » qui vient directement éclairer le capteur (transmission
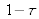 ) à travers le cube (Tc
= 50%). En première approximation, on supposera qu'il n'y a pas de pertes dans le coupleur.
) à travers le cube (Tc
= 50%). En première approximation, on supposera qu'il n'y a pas de pertes dans le coupleur.
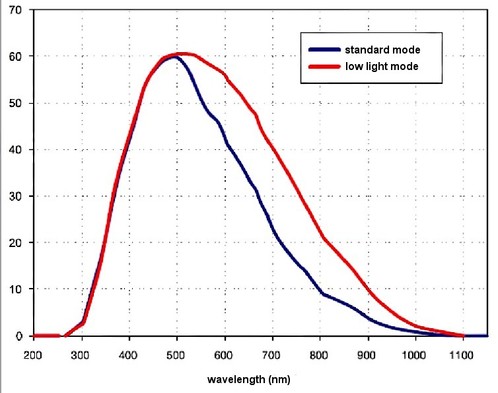
La Figure 3 donne la courbe d'efficacité quantique du capteur, utilisé en mode standard.
Dans cet exercice, on s'intéresse à chiffrer la puissance PL et l'énergie QL nécessaires du laser. Pour fixer les ordres de grandeur, on s'intéressera à la somme des énergies lumineuses des faisceaux objet et référence, évaluée au niveau du capteur.
Constantes fondamentales :
-
constante de Planck : h = 6,6256×10-34 J.s
-
vitesse de la lumière : c = 299792458 m.s-1
-
constante de Boltzmann : k = 1,380662×10-23 J.K-1
-
charge de l'électron : q = 1,60217653×10-19 coulomb
-
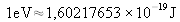
Question
L'image de la zone d'intérêt doit couvrir entièrement le capteur. Quel doit être le grandissement transversal g entre le plan de l'objet et le plan d'enregistrement ? En déduire la position de la zone d'écoulement par rapport à la caméra.
Question
Déduire de la question précédente la résolution spatiale dans le plan de l'objet.
Question
Donner la relation entre PL
, QL
et
 . Quel est l'éclairement produit par le laser dans le plan de l'objet ?
. Quel est l'éclairement produit par le laser dans le plan de l'objet ?
Question
L'objet reçoit l'éclairement laser et on le considère comme un diffuseur lambertien [1]. Quelle est la luminance LS
produite par cet objet ? Exprimer Lo
en fonction de
 , QL
,
, QL
,
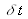 et
et
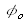 .
.
Question
Calculer l'éclairement produit par l'objet dans le plan du capteur d'images.
Question
Calculer le nombre de photo-électrons obtenus pour 1 pixel, Ne-
, pendant la durée de l'impulsion laser en fonction de ER
, px
, py
,
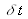 ,
,
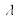 , h, c,
, h, c,
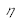 ; puis exprimer Ne-
en fonction de QL
, px
, py
,
; puis exprimer Ne-
en fonction de QL
, px
, py
,
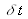 ,
,
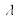 , h , c ,
, h , c ,
 , Topt
,
, Topt
,
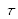 , Tc
,
, Tc
,
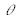 , N et
, N et
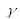 .
.
Quelle est la valeur de l'efficacité quantique (
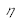 ) du capteur d'images ?
) du capteur d'images ?
Question
Quel est le nombre de photo-électrons générés par le faisceau référence ? On supposera que toute l'énergie laser éclaire la surface du capteur.
Question
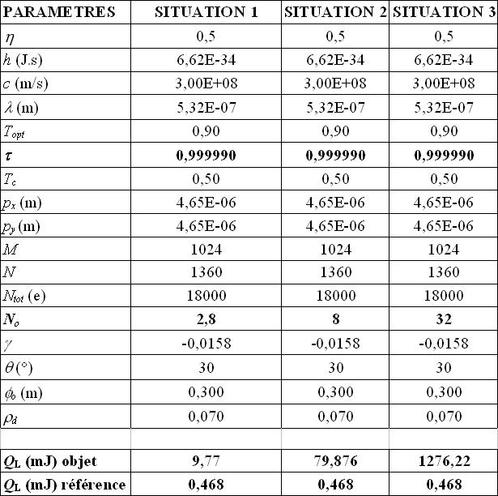
Exprimer la valeur de l'énergie laser QL pour saturer au moins un quart de chaque pixel, pour chaque faisceau (objet et référence). Calculer numériquement QL pour No = 2,8, No = 8 et No = 32. Présenter les résultats dans un tableau puis commenter ces résultats.
Question
Quelle stratégie adopter pour l'acquisition d'images si on souhaite étudier l'objet en vibration entre 5 kHz et 10 kHz ?