Modification de la Phase : mécanisme
La sensibilité du capteur est dépendante du degré de rotation de polarisation induite par le mesurande et de la rotation minimale détectable. L'influence du mesurande sur l'état de polarisation peut être déterminée comme suit. La phase d'une onde guidée par une fibre de longueur L est :
où
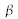est la constante de propagation du mode, neff est son indice effectif et
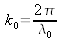le vecteur d'onde dans le vide, avec
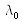la longueur d'onde dans le vide. La différence de phase entre deux modes guidés de la fibre après une longueur L est :
où
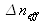est la différence entre les indices effectifs des deux modes de polarisation.
Effet d'une déformation mécanique
Supposons que la fibre soit soumise à une déformation mécanique extérieure
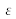. Le déphasage créé par
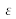est proportionnel à la longueur de la fibre exposée à cette déformation. Il est donc important de considérer la réponse du capteur par unité de longueur. On a donc :
où D et n sont respectivement la dimension transverse et profil d'indice de la fibre.
Le premier terme de l'équation 3 décrit l'effet photoélastique qui est la variation de l'indice de réfraction d'un matériaux en fonction de la déformation mécanique. Dans le cas des fibres circulaires normales, cette variation peut être calculée par l'expression suivante :
où
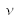est le coefficient de Poisson de la silice supposé identique pour le cœur et le cladding, et p11, p12
sont les coefficients élasto-optique de la silice [
].
Le second terme de l'équation 3 est relatif à la variation de la section de la fibre soumise à une déformation mécanique. Cette modification de la section va affecter les indices effectifs des modes et donc leurs différences (i.e.
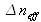). Il a été montré que cette contribution à la variation de la différence de phase est très faible et peut être négligée dans la pratique.
Le dernier terme de l'équation 37 décrit la variation de longueur de la fibre sous l'effet de la déformation mécanique.
Effet de la température
Une étude similaire à la précédente peut être menée pour décrire les changements induits par la température. La variation du déphasage dû à la température (T) est obtenue par :
L'équation 5 comme la 3 comporte les mêmes deux premiers termes relatifs aux changements des paramètres opto-géométriques de la fibre (n et D) engendrant une variation de
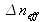. Les variations de l'indice de réfraction sont dues à l'effet thermo-optique. Le troisième terme traduisant ici la compression ou l'expansion thermique, qui a pour valeur :
où
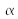est le coefficient dilatation thermique.
La variation du déphasage est principalement due à la modification de l'indice de réfraction avec la température.
Les équations 3 et 5 sont utilisées pour calculer les sensibilités thermique et mécanique des fibres circulaires. Pour les fibres biréfringentes, le calcul des sensibilités est plus compliqué à cause de la complexité des formes et des matériaux constituant la fibre. On a donc souvent recours à la détermination expérimentale de ces sensibilités pour les fibres les plus exotiques.