Fréquence linéaire

Nous mettons ici en évidence l'utilité de la transformation de Fourier fractionnaire à l'analyse des signaux à dérive de fréquence linéaire appelés aussi chirps. Ces signaux sont caractérisés par une évolution linéaire de leur contenu spectral. Considérons le signal harmonique défini par :

Sa fréquence instantanée est :

où est la phase de  . Si la fréquence instantanée 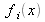 est une constante pour tout alors le signal  est dit stationnaire . La Transformation de Fourier classique est bien adaptée à l'analyse de tels signaux. En effet, une TF de  permet de mettre en évidence de manière synthétique ses propriétés spectrales. Sa TF est une impulsion de Dirac centrée à la fréquence  .

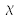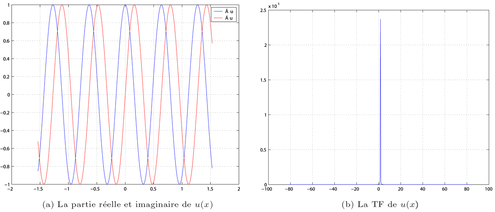
Figure 1 : Représentation de ainsi que sa Transformation de Fourier

Les figures 1.(a) et (b) représentent  et sa transformée de Fourier. Si la fonction  est une fonction à dérive de fréquence linéaire telle que :

sa transformée de Fourier fractionnaire est égale à :

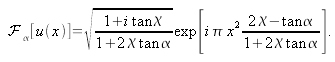
Pour 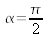 on trouve la transformée de Fourier classique, qui est encore une fonction chirp. Par contre pour  et en utilisant l'égalité  :

on obtient :

Cette fois, la distribution de Dirac est centrée à l'origine des coordonnées. La fonction  est donc une fonction centrée.

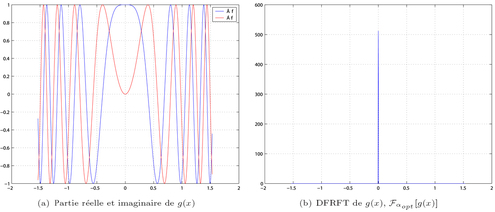
Figure 2 : Représentation de 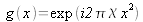ainsi que sa transformation de Fourier fractionnaire d'ordre optimal

Les figures 2 (a) et (b) illustrent cette propriété. C'est d'ailleurs cette propriété qui nous permettra de réaliser une métrologie puisque les phénomènes de diffraction dans l'approximation de Fresnel sont à dérive de fréquence linéaire.