Régime de réflexion totale

Si on s'intéresse à la réflexion totale entre le substrat et la couche, l'expression de l'angle critique doit être réécrite en fonction des valeurs accessibles expérimentalement et donc définies dans le milieu d'incidence (milieu I ou 0). Nous notons 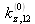la valeur particulière de 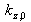correspondant à l'angle incident où va se manifester cette réflexion totale. Selon l'expression vue précédemment nous obtenons :

La réflexion totale entre la couche et le substrat est donc mesurée dans le milieu incident au même angle que celui obtenu sur le substrat nu 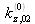. Par contre en présence de la couche, une autre valeur particulière de 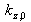existe et correspond au phénomène de réflexion totale sur la couche dans le milieu incident. L'angle critique correspondant s'obtient avec :

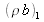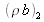Plusieurs cas peuvent être envisagés quand on compare ces deux angles critiques, ce qui revient à comparer et . Quelle que soit la relation entre ces deux potentiels, un plateau de réflexion totale est mesuré aux petits angles ainsi le coefficient de réflexion global r doit être de module unité.

• Lorsque 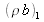< 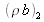, la réflexion totale à l'interface entre la couche et le substrat va avoir lieu en premier quand l'angle d'incidence diminue puisque 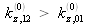. Entre ces deux valeurs particulières de 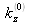, il y a réflexion totale sur le substrat mais pas encore sur la couche pleine, ainsi 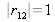et 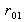est réel.

  Posons : 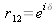, 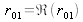et 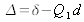pour pouvoir reformuler :

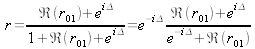
  ce qui conduit à :

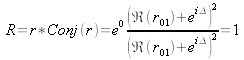
  Aux angles encore plus faibles, apparaît en plus la réflexion totale sur la première interface rencontrée 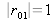. Dans ce cas, 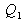et 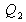étant des imaginaires purs, r12 est purement réel mais n'est plus de module unité puisque toute l'énergie de l'onde évanescente pénétrant la couche n'arrive pas jusqu'au substrat.

  En posan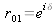t : et 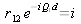un réel, on obtient :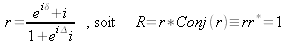

  

• Lorsque 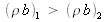, la réflexion totale sur la couche se manifeste avant celle sur le substrat lorsque 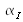décroît. Pour 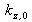compris entre 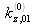et 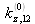, on a donc 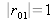et une onde évanescente (mode non propagatif) s'étend jusqu'au substrat ( 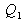est un imaginaire pur). Comme précédemment le formalisme utilisé permet d'expliquer la présence d'un plateau de réflexion totale.