Evaluation of the optical path difference
For any point S' in the source, the optical path difference at point M at observation coordinates (x, y) can be broken down into two parts. The first one takes into account the optical path difference introduced between the source and the secondary sources, while the second one takes into account the optical path difference between the secondary sources and observation point M.
with:
Under the condition that the transversal lengths remain small despite the distance separating the primary source and the two secondary sources
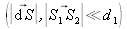, we can write:
which gives:
We can therefore deduce that:
where
For point S, and the secondary sources placed symmetrically, we find that:
Based on the previous expressions, we can note that optical path difference can also be written as:
where
,
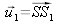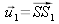and
.
This expression leads us to the following conclusions:
-
There is no variation between the optical path difference and the width of the source when:
-
The shift
is perpendicular to the vector
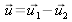. In this case, the source point can be replaced by a source slit without affecting the fringe contrast. -
If the two vectors
and
are collinear, the interferometer is said to be amplitude-splitting, and a wide source can be used.
-
-
The optical path difference in S' is expressed as:
where
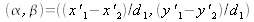are the apparent angles through which the two secondary sources are seen from the source's center S in both transversal directions of the reference axes. -
When the vector
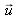is parallel to the shifting vector
, the optical path difference is expressed as:
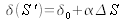
Fringe contrast decrease will occur, if the variation in optical path difference is equal to
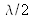, i.e.:
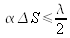
which corresponds to an angular width of spatial coherence of the order:
.