Interferences: fundamentals

Illumination at an observation point

The source element dXdY gives to observation point M of the abscissa (x, y) the intensity:

i.e. by replacing 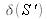with the expression:

For all of the source, the different points emit incoherently:

i.e.:

[zoom...]

This expression can be rewritten as:

we note that:

where 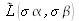is the Fourier transform of the source's light distribution. This result means that the interferogram observed in the presence of an extended source is directly related to the Fourier transform of the sources light distribution.

For 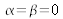, we have 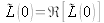and the interferogram becomes:

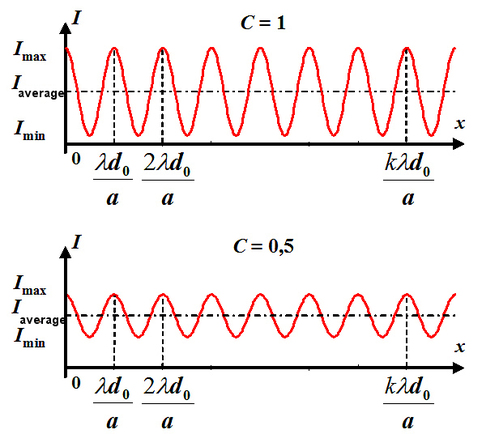
The modulation term of the cosine is referred to as the degree of spatial coherence of the source. We note the spatial degree of coherence:

This result constitutes the Van Cittert–Zernike Theorem [2]: it demonstrates that the degree of spatial coherence at point M on the screen is equal to the value of the Fourier transform of the source's light distribution that is calculated for the angular coordinates where the secondary sources are seen from the center of the primary source. The degree of spatial coherence is normalized in such a way that if S1 = S2, the spatial coherence is obviously perfect if the secondary sources are superimposed.

Note that unlike temporal coherence, the contrast does not depend on the value of the optical path difference, but that instead it depends on the angle from which the secondary sources are seen from the center of the source. The contrast diminishes as angles increase. (figure 15).

Figure 15: For a source of a given dimension the fringe contrast is constant [zoom...]

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Two types of interferometersExamples