Glass Corner

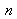The prismatic blade of apex angle of index (figure 8) is lit with almost normal incidence by a monochromatic and extended source.

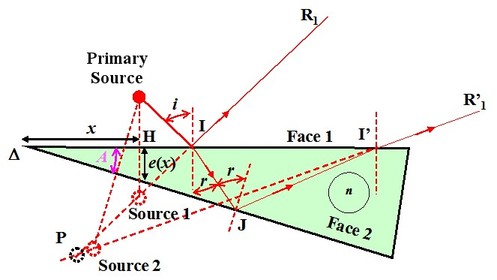
A part of the incident beam 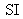is reflected on the first diopter surface and a second part is refracted in 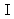then reflected on the second diopter surface in before it is refracted in 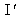. Both beams 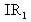and stemming from the same incident beam converge in 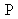where interfringes are formed. Interferences are located close to the blade, around point 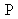. On figure 8, the incidence angle has been considerably incremented, as well as angle for more clarity; in reality angle order of magnitude equals of arc .In almost regular incidence, points 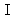and are very close and the blade thickness can locally be considered as constant and equal to 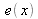. Thus, the difference of optical path between beams and is sensibly equal to the one given by blade with parallel sides placed in the air, lit under normal incidence:

As the corner index is 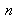. The reflection in 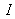occurs on a more refringent medium than the incident medium when the second reflection in occurs on a less refringent medium than the incident medium of index 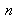 ; both reflections are not of the same kind, which justifies the additional term . For any point of a bright interference fringe, the course difference verifies:

For a given blade, the wavelength and the index are constant; the points corresponding to the same state of interferences, consequently at the same order of interferences 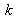verify:

Thus, interferences fringes are lines parallel to the intersection line 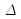of both diopters. These fringes are called “same thickness fringes”. The interfringe 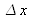is obtained for a variation of order 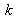of one unity hence:

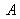Considering that because angle is weak, we obtain:

The interfringe decreases when angle 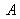increases.