Minimum or maximum

Let us consider two points in space A and B in an homogeneous medium. Within a given point M, a plane surface, of which the normal is the bisector of the (AMB) angle, allows the AM ray to reflect towards MB, the light therefore follows the AMB path. For a tangent spherical surface in M to the plane mirror the result is identical. For these two surfaces, the ray reflecting itself in M alone passes through B.

The figure below is situated on the plane going through A, B and M. We traced the tangent ellipse in M to the plane mirror of which the focus are A and B. Any point M0 of the ellipse is such that L0 = AM0 + M0B is constant.

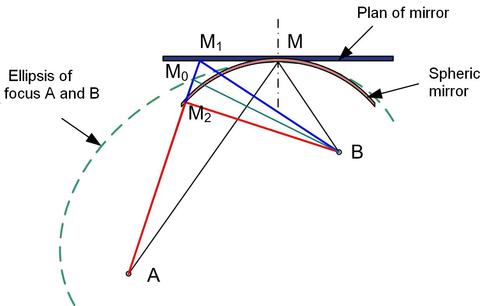
The optical paths for current points on the surfaces are :

Plane mirror : L1 = AM1+M1B

Spherical plane : L2 = AM2+M2B

The spherical plane having a beam curvature inferior to that of the ellipsis in M, it is evident that : L2 < L0 < L1

For the plane mirror L is minimal. For the spherical mirror L is maximal.