Plane mirrors

Let an object point be A and its projection on the mirror H. Any ray out of A follows the law (16). The prolongation of the reflected ray cuts the line AH at a point AH'. On figure 22 we easily demonstrate that if the absolute values of i1 and i2 are equal, those of i3 and i4 also are and HA=HA'.

Point A' is the symetry of A in relation to the mirror.

This is true for all luminous rays issued of A, the image is stigmatic, figure 22 show a real object and a virtual image. If we inverse the direction of the luminous rays, the object becomes A', virtual, and the image becomes A, real.

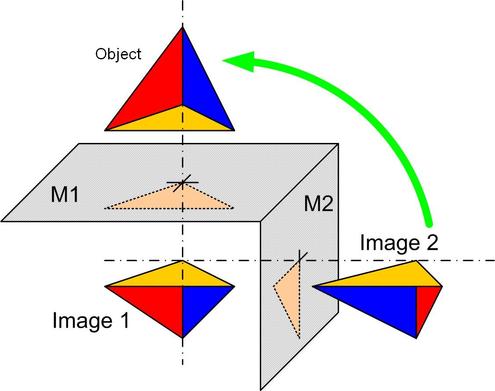
The image of an object in volume by a plane mirror has identical dimentions to the object but is not superimposable to it. It is said that it is a left handed image. A second image obtained from the first by a second mirror becomes superimposable to the object, by translation or rotation as in figure 23, it is said that it is a right handed image.

In such visual intruments as binoculars and spectacles, a paired number of reflexions ensures a right handed image.