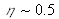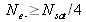Exercise : pulsed laser lighting
To define an interferometric sensor, we need the photometric balance of the object illumination system and the image capture.
The object of interest is in albedo steel
 and with a diameter of
and with a diameter of
 . The imagery objective has a focal length of f' = 18 mm, a transmission of Topt = 90% and has an aperture ring with the following apertures: No = {2.8 ;4 ;5.6 ;8 ;11.3 ;16 ;22.6 ;32}. For layout reasons, the object will be illuminated with a medium incidence of
. The imagery objective has a focal length of f' = 18 mm, a transmission of Topt = 90% and has an aperture ring with the following apertures: No = {2.8 ;4 ;5.6 ;8 ;11.3 ;16 ;22.6 ;32}. For layout reasons, the object will be illuminated with a medium incidence of
 .
.
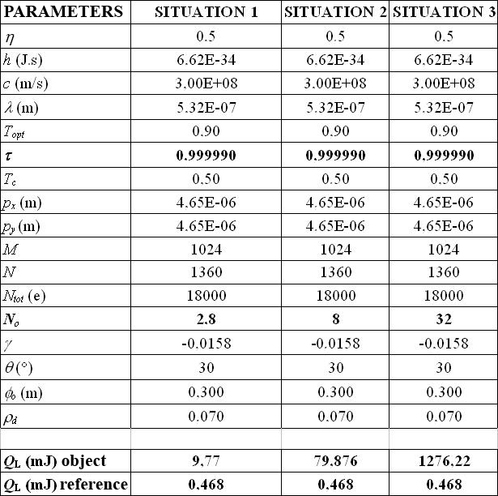
The CCD sensor used has a size of MxN = 1024´1360 pixels (of a size of px = py = 4.65 mm). Each pixel contains Nsat = 18,000 electrons at the saturation point and the pixel frequency is of 20 MHz. The integration time can be adjusted between 5 ms and 65 s.
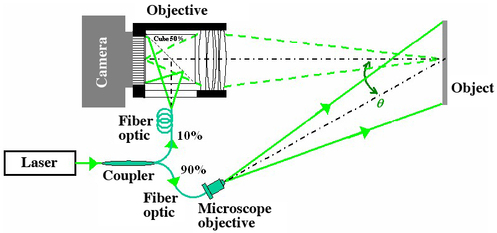
We use an NdYAG pulsed laser doubled with a KDP crystal. The laser pulses delivered have a duration of 20 ns. The laser can have a rhythm between 30 and 60 Hz. The experimental device of laser imagery is described in Figure 2. A variable transmission coupler (not described here) separates the laser wave in an "object illumination" (transmission
 ) and a "reference" part that illuminates directly the sensor (transmission
) and a "reference" part that illuminates directly the sensor (transmission
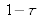 ) through the cube (Tc
= 50%). For the first rough estimate, we will suppose that there's no loss in the coupler.
) through the cube (Tc
= 50%). For the first rough estimate, we will suppose that there's no loss in the coupler.
In Figure 3, we can see the sensor's quantum efficiency curve, when used in standard mode.

In this exercise, the aim is to assess the power PL and energy QL needed by the laser. To decide on the orders of magnitude, we will focus on the sum of the light energies of the object and reference beams.
Fondamental constants:
-
Planck's constant: h = 6.6256×10-34 J.s
-
Speed of light: c = 299792458 m.s-1
-
Boltzmann's constant: k = 1.380662×10-23 J.K-1
-
Electron charge: q = 1.60217653×10-19 coulomb
-

Question
The image of the zone we are interested in must cover the entire sensor. What must the lateral magnification g between the object plane and the recording plane be? Deduce the draining zone position compared to the camera.
Question
Deduce from the previous question the spatial resolution inside the object plane.
Question
Give the relation between PL
, QL
and
 . What is the illumination produced by the laser in the object plane?
. What is the illumination produced by the laser in the object plane?
Question
The object receives the laser illumination and is considered as a Lambertian diffuser [1]. What is the luminance LS
produced by this object? Express Lo
according to
 , QL
,
, QL
,
 and
and
 .
.
Question
Calculate the illumination produced by the object in the image sensor plane.
Question
Calculate the number of photoelectrons obtained for 1 pixel, Ne-
-, for the duration of the laser impulse, according to ER
, px
, py
,
 ,
,
 , h, c,
, h, c,
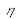 ; then express Ne-
according to QL
, px
, py
,
; then express Ne-
according to QL
, px
, py
,
 ,
,
 , h , c ,
, h , c ,
 , Topt
,
, Topt
,
 , Tc
,
, Tc
,
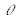 , N et
, N et
 .
.
What is the value of the image sensor's quantum efficiency (
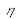 ) ?
) ?
Question
What is the number of photoelectrons generated by the reference beam? We'll suppose that all the laser energy illuminates the sensor's surface.
Question
Express the value of the laser energy QL in order to saturate at least a quarter of each pixel, for each beam (reference beam and object beam). Calculate QL for No = 2,8, No = 8 and No = 32. Display the results in a table and give your comments on them.
Question
What is the best strategy to adopt in order to acquire images if one wish to study the object while it is vibrating between 5 kHz and 10 kHz?