Interférogramme en lumière polychromatique
Dans le cas où les deux ondes sont issues d'une source polychromatique, la représentation spectrale de la source ne correspond plus à une raie unique localisée en
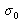, nombre d'onde de la source (ou bien en
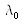longueur d'onde ou
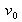fréquence ou
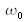pulsation). Le spectre, ou densité spectrale d'énergie, noté
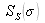, est composé d'une enveloppe
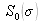centrée sur le nombre d'onde moyen
.
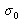La figure 8 illustre la représentation spectrale d'une source.
![[zoom...]](javascript:window.open(%22../res/fig_08_C_2.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
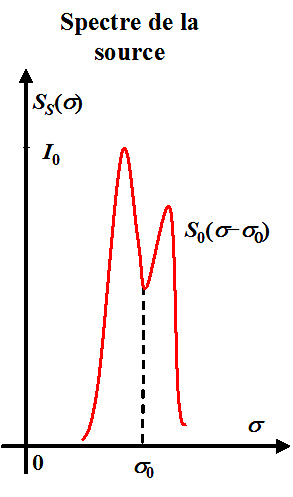
D'après le paragraphe "Signal d'interférences", le signal d'interférence peut s'écrire synthétiquement :
où :
où
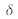est la différence de chemin optique entre les deux ondes. Le signal devient désormais :
L'interférogramme (nom donné à la représentation du signal d'interférences) s'écrit sous forme intégrale [2] :
Le spectre de la source, c'est à dire la représentation spectrale de la source, est par nature réel et nul pour toute valeur
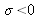. Il vient donc, puisque
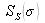est réel :
où
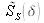est la transformée de Fourier de la densité spectrale d'énergie de la source, et on constate que :
Ce résultat signifie donc que l'interférogramme observé en présence de lumière polychromatique est directement lié à la transformée de Fourier du spectre de la source.
Qualitativement, si la source a un spectre étroit, alors l'interférogramme sera étendu et si la source a un spectre très large alors l'interférogramme sera très localisé au voisinage de
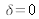. Écrivons le spectre de la façon suivante :
où
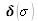est la distribution de Dirac et * signifie convolution. On obtient alors :
En
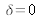, on a
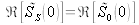et la répartition d'intensité en fonction de
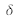devient :
Le terme de modulation du cosinus s'appelle le degré de cohérence temporelle de la source. On note le degré de cohérence temporelle :
Ce résultat constitue le théorème de Wiener–Kinchine [2] : il démontre que le degré de cohérence temporelle au point M de l'écran est égal à la valeur numérique de la transformée de Fourier de la densité spectrale d'énergie de la source, calculée à la valeur de la différence de marche au point M. Le degré de cohérence temporelle est normalisé de sorte que
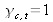si la source est monochromatique, la cohérence temporelle étant évidemment parfaite si la source n'émet qu'une seule radiation.