
Illustrations
Considérons quelques sources et l'interférogramme associé [ ] :
Cas d'une radiation monochromatique
Dans le cas où le spectre n'est composé que d'une onde monochromatique de longueur d'onde
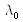 , on peut modéliser le spectre par :
, on peut modéliser le spectre par :
L'enveloppe spectrale est donc restreinte à une distribution de Dirac
 . La transformée de Fourier de
. La transformée de Fourier de
 est
est
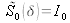 . Le degré de cohérence est :
. Le degré de cohérence est :
La longueur de cohérence de la source est donc infinie puisque le degré de cohérence n'est pas sommable. Le signal d'interférences est alors :
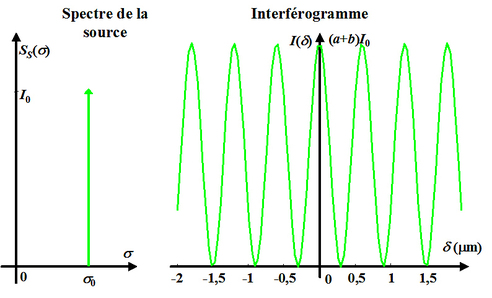
Le spectre et l'interférogramme associé sont représentés sur la figure 9 pour une source monochromatique de longueur d'onde
 .
.
Cas d'un doublet
Si la source comporte deux radiations monochromatiques de nombres d'onde
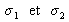 avec
avec
 et de même amplitude
et de même amplitude
 , on peut modéliser son spectre par :
, on peut modéliser son spectre par :
Dans ce cas, le nombre d'onde moyen du spectre est
 et l'intervalle spectral est
et l'intervalle spectral est
 . On a alors :
. On a alors :
et puisque
 est l'enveloppe du spectre (voir figure 8), nous avons :
est l'enveloppe du spectre (voir figure 8), nous avons :
dont la transformée de Fourier est :
Le degré de cohérence temporelle est alors :
Le signal d'interférences s'écrit :
L'interférogramme présente des battements. Ils sont représentés sur la figure 10 dans le cas où
 et
et
 .
.
Pour ce cas idéal où la largeur de raie est considérée infiniment mince, la longueur de cohérence de la source est également infinie puisque le degré n'est pas sommable. Cependant, dans la réalité, il faudrait considérer la largeur de chaque raie ainsi qu'un modèle pour le profil de raie. On trouverait alors que le degré de cohérence est sommable et que la longueur de cohérence n'est pas infinie mais qu'elle dépend fortement de la largeur de raie.
Cas d'une répartition spectrale rectangulaire
Si on considère une répartition spectrale uniforme sur l'intervalle
 centré sur
centré sur
 et d'amplitude
et d'amplitude
 , le spectre est décrit par la fonction :
, le spectre est décrit par la fonction :
et :
dont la transformée de Fourier est :
Dans tout ce qui suit la fonction sinuscardinal est définie par :
La répartition d'intensité s'écrit :
Le degré de cohérence d'une telle source est donc :
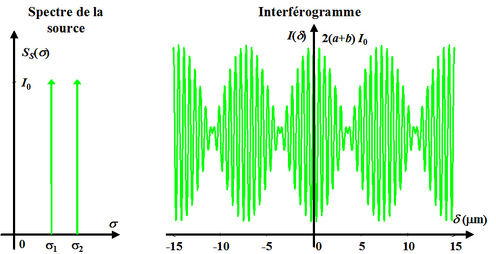
Le spectre et l'interférogramme sont représentés sur la figure 11 dans le cas où
 et
et
 (modèle simplifié de lumière blanche).
(modèle simplifié de lumière blanche).

La longueur de cohérence est obtenue en calculant :
ce qui donne :
Avec les valeurs numériques, on trouve
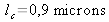 et
et
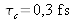 .
.
Cas d'une raie monochromatique à répartition spectrale lorentzienne
Cette situation correspond à l'élargissement des raies réelles par l'effet Doppler dû à l'agitation thermique dans le milieu d'émission. L'intensité spectrale peut être modélisée par :
où
 représente la largeur de la raie à mi hauteur.
représente la largeur de la raie à mi hauteur.
L'enveloppe de la répartition spectrale est décrite par :
dont la transformée de Fourier est :
Le degré de cohérence temporelle est :
L'intensité a pour expression :
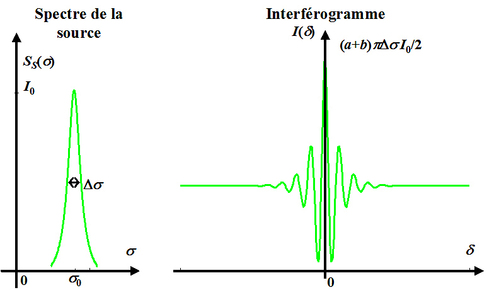
Plus la raie est large et plus la décroissance de l'interférogramme est rapide, donc plus vite il n'y a plus possibilité d'observer la modulation du signal. Le spectre et l'interférogramme sont représentés schématiquement sur la figure 12.
La longueur de cohérence est :
ce qui donne :
Par exemple, dans le cas d'une diode laser pour laquelle
 et
et
 on a
on a
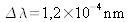 . On calcule que
. On calcule que
 et
et
 . La représentation graphique de l'interférogramme sur une variation de différence de marche égale à la longueur de cohérence n'est pas possible en raison du trop grand nombre d'oscillations du
. La représentation graphique de l'interférogramme sur une variation de différence de marche égale à la longueur de cohérence n'est pas possible en raison du trop grand nombre d'oscillations du
 sous la courbe de modulation.
sous la courbe de modulation.