Éclairement en un point d'observation
L'élément de source dXdY donne au point M d'observation d'abscisse (x, y) l'intensité :
soit en remplaçant
par son expression :
Pour l'ensemble de la source, les différents points émettent de façon incohérente :
soit :
Cette expression est réécrite :
on constate que :
où
est la transformée de Fourier de la répartition de luminance de la source. Ce résultat signifie que l'interférogramme observé en présence d'une source étendue est directement lié à la transformée de Fourier de la répartition de luminance de la source.
Pour
, on a
et l'interférogramme devient :
Le terme de modulation du cosinus s'appelle le degré de cohérence spatiale de la source. On notera le degré de cohérence spatiale
Ce résultat constitue le théorème de Van Cittert–Zernike [2] : il démontre que le degré de cohérence spatiale au point M de l'écran est égal à la valeur numérique de la transformée de Fourier de la répartition de luminance de la source, calculée aux coordonnées angulaires sous lesquelles les sources secondaires sont vues depuis le centre de la source primaire. Le degré de cohérence spatiale est normalisé de sorte que
si S1 est confondue avec S2, la cohérence spatiale est évidemment parfaite.
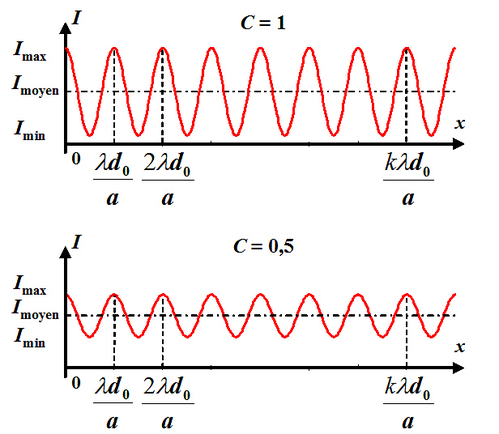
Contrairement au cas de la cohérence temporelle, le contraste ne dépend pas de la valeur de la différence de marche, il dépend de l'angle sous lequel sont vus les sources secondaires depuis le centre de la source. Il diminue quand les angles
augmentent (voir illustration figure 15).
![[zoom...]](javascript:window.open(%22../res/fig_15_C_2.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}