Illustration

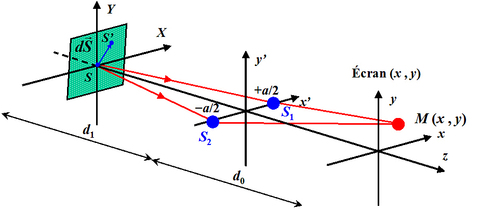
On s'intéresse à la baisse de contraste induite par une source étendue de forme circulaire émettant une radiation monochromatique 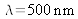. La figure 16 donne les notations. On notera R le rayon de la source.

La source circulaire a une luminance uniforme que l'on décrira par la fonction suivante :

La transformée de Fourier de la répartition angulaire de la source est donnée par :

La source possède une symétrie circulaire, nous pouvons effectuer une transformation en coordonnées polaires à la fois sur (X , Y) et sur 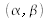, soit :

ainsi,

ou encore :

Compte tenu que :

J0 étant la fonction de Bessel de première espèce d'ordre 0, on a :

D'après la définition de la fonction luminance, il découle :

En posant 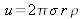, on obtient :

Avec l'égalité :

J1 étant la fonction de Bessel d'ordre 1 telle que 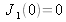, on obtient finalement :

Comme nous avons :

le degré de cohérence spatiale de la source circulaire s'écrit finalement :

Le degré de cohérence spatiale de la source circulaire est de la forme 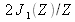où 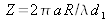. La figure 17 montre le profil du degré de cohérence spatiale de la source de forme circulaire en fonction de la valeur de Z exprimée en radians.

Le Tableau 2 donne les valeurs de Z pour les maxima, minima et zéros successifs du degré de cohérence.

Les zéros du degré de cohérence ne sont pas équidistants. La première annulation du contraste est obtenue pour :

soit pour un écart entre les sources secondaires égal à :

On rappelle que R représente le rayon de la source.

En fonction du diamètre angulaire 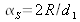sous lequel on voit la source depuis le plan des sources secondaires, nous obtenons

A titre d'exemple numérique, considérons le cas du Soleil, pour lequel l'angle apparent sous lequel il est observé depuis la terre est 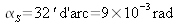. La relation précédente donne pour . Si on veut observer des interférences contrastées au point M d'un écran, il faudra que les deux sources secondaires ne soient pas distantes de plus de cette valeur. La lumière qui provient du Soleil possède donc une très faible cohérence spatiale.

Pour des sources secondaires de même amplitude, le signal d'interférences au point M sur l'écran s'écrit finalement sous la forme :

La figure 18 montre les interférogrammes obtenus dans le plan de l'écran pour différentes valeurs du degré de cohérence.

Le contraste des franges évolue en fonction du rayon R de la source suivant la courbe de la figure 17. Pour une faible valeur de R, le contraste des franges est sensiblement égal à l'unité. Lorsqu'on augmente R, le contraste diminue puis devient nul pour 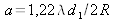. Ensuite, il devient négatif et les franges brillantes occupent alors la position des franges sombres et réciproquement ; c'est l'inversion du contraste que l'on peut observer assez facilement sur la figure 18, le contraste étant cependant assez faible en valeur absolue 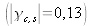. Si on continue à augmenter la valeur de R, les franges deviennent de moins en moins visibles et finissent par complètement disparaître.

On s'intéresse maintenant à la baisse de contraste induite par une source étendue de forme rectangulaire. La figure 19 illustre les notations. On notera 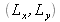les dimensions de la source.

La source circulaire a une luminance uniforme que l'on décrira par la fonction suivante :

La transformée de Fourier de la répartition de luminance de la source est donnée par :

Compte tenu de la définition de la fonction luminance, nous avons :

Cette expression s'intègre facilement et on trouve :

Puisque les sources secondaires sont réduites à deux points, , nous avons :

Pour le cas illustré sur la figure 19, le degré de cohérence spatiale de la source de forme rectangulaire s'écrit finalement :

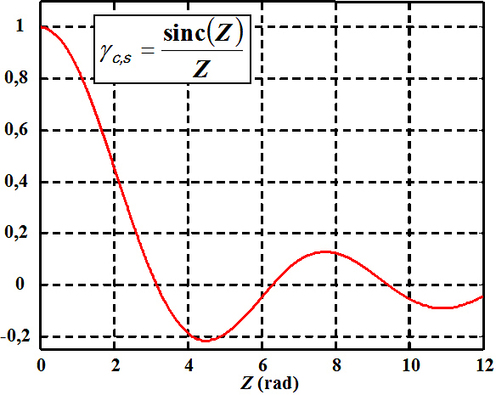
Le degré de cohérence spatiale de la source rectangulaire est de la forme d'une fonction sinuscardinal. La figure 20 montre le profil du degré de cohérence spatiale de la source de forme rectangulaire en fonction de la valeur de Z exprimée en radians.

Les zéros du degré de cohérence sont équidistants. Le contraste s'annule pour :

Le premier zéro est obtenu pour un écart entre les sources secondaires égal à :

Cette expression donne une estimation de la largeur de cohérence spatiale de la source.