
Interféromètre de Twyman-Green
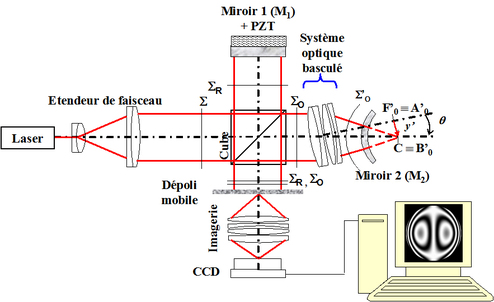
L'interféromètre de Twyman-Green est une variante de l'interféromètre de Michelson. Il est utilisé industriellement pour le contrôle interférométrique des surfaces optiques non planes ou des objectifs à lentilles ou miroirs. La figure 22 présente le dispositif de Twyman-Green.
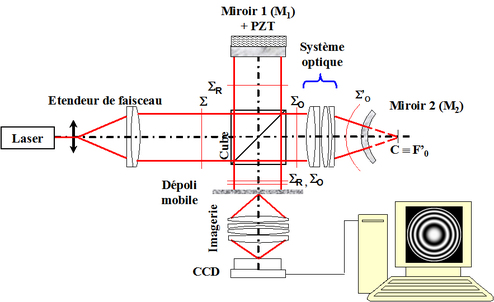
Le miroir plan
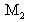 du Michelson est remplacé par un assemblage comprenant le système optique à étudier et un miroir sphérique. Le miroir sphérique est placé de sorte que son centre de courbure
du Michelson est remplacé par un assemblage comprenant le système optique à étudier et un miroir sphérique. Le miroir sphérique est placé de sorte que son centre de courbure
 soit confondu avec le foyer paraxial du système optique
soit confondu avec le foyer paraxial du système optique
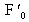 . Par aller retour dans l'interféromètre les franges sont visibles sur l'écran qui est désormais remplacé par un dépoli tournant. Le système optique d'imagerie forme l'image des franges sur le détecteur matriciel
. Par aller retour dans l'interféromètre les franges sont visibles sur l'écran qui est désormais remplacé par un dépoli tournant. Le système optique d'imagerie forme l'image des franges sur le détecteur matriciel
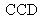 ou
ou
 . Si le dépoli était statique, il génèrerait un « speckle » (phénomène aléatoire) qui brouillerait les franges d'interférences. Le dépoli est donc généralement monté sur un moteur qui le fait tourner à une vitesse suffisante pour que le speckle soit moyenné dans le temps d'intégration du capteur d'images, de sorte que les grains de speckle n'apparaissent plus visibles sur l'image des franges.
. Si le dépoli était statique, il génèrerait un « speckle » (phénomène aléatoire) qui brouillerait les franges d'interférences. Le dépoli est donc généralement monté sur un moteur qui le fait tourner à une vitesse suffisante pour que le speckle soit moyenné dans le temps d'intégration du capteur d'images, de sorte que les grains de speckle n'apparaissent plus visibles sur l'image des franges.
Le miroir plan de référence
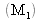 est monté sur un transducteur piézo-électrique qui permet de translater légèrement
est monté sur un transducteur piézo-électrique qui permet de translater légèrement
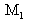 et d'appliquer la méthode du décalage de phase pour calculer la phase optique des interférences. Ce dernier aspect de l'interféromètre ne sera pas détaillé ici et nous invitons le lecteur à se reporter au cours « Interférométrie et démodulation de franges ».
et d'appliquer la méthode du décalage de phase pour calculer la phase optique des interférences. Ce dernier aspect de l'interféromètre ne sera pas détaillé ici et nous invitons le lecteur à se reporter au cours « Interférométrie et démodulation de franges ».
La surface d'onde plane
 issue du laser est séparée en deux surfaces d'ondes planes
issue du laser est séparée en deux surfaces d'ondes planes
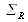 et
et
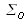 . Par aller retour sur le miroir
. Par aller retour sur le miroir
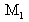 , la surface d'onde de référence
, la surface d'onde de référence
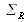 reste plane, mais elle peut éventuellement être inclinée par un basculement du miroir
reste plane, mais elle peut éventuellement être inclinée par un basculement du miroir
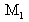 . La surface d'onde objet
. La surface d'onde objet
 est transformée en onde sphérique par le système optique, si il est parfait, puis par réflexion sur le miroir sphérique et retour dans le système optique elle redevient plane. En sortie de l'interféromètre il se produit des interférences entre la surface d'onde plane idéale issue du miroir
est transformée en onde sphérique par le système optique, si il est parfait, puis par réflexion sur le miroir sphérique et retour dans le système optique elle redevient plane. En sortie de l'interféromètre il se produit des interférences entre la surface d'onde plane idéale issue du miroir
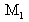 par aller retour et la surface d'onde qui est produite par l'aller retour dans le système optique. L'analyse des franges d'interférences permet de quantifier le défaut introduit par le système optique.
par aller retour et la surface d'onde qui est produite par l'aller retour dans le système optique. L'analyse des franges d'interférences permet de quantifier le défaut introduit par le système optique.
Aberration du composant optique
Si le système optique testé est parfait, la surface d'onde issue du trajet aller-retour système-miroir 2 est plane. Dans le cas contraire, elle présente de « l'aberration » due au système optique [ ]. Si le système optique est aberrant, la surface d'onde en sortie du système n'est pas sphérique mais elle présente un écart normal d'aberration qui est la différence entre la surface d'onde réelle et la surface d'onde sphérique idéale (voir la figure 23).
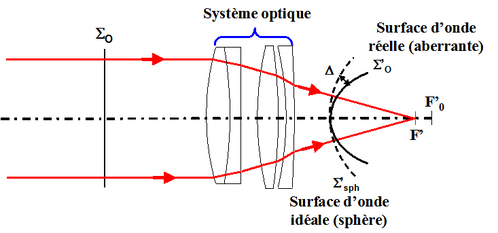
L'écart normal d'aberration dépend du type d'aberration du composant. L'interféromètre de Twyman-Green permet de mettre en évidence facilement les aberrations primaires suivantes [ ] :
aberration sphérique du 3ème ordre
aberration de coma du 3ème ordre
aberration d'astigmatisme du 3ème ordre
L'expression analytique de l'écart normal sera donnée dans les exemples ci après.
L'écart normal fait toujours référence à la différence entre la surface d'onde réelle et la surface de référence qui peut être soit plane soit sphérique.
Contribution des deux miroirs
Le bras de référence est composé du miroir plan
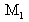 monté sur le transducteur piézoélectrique. A priori, le front réfléchi qui interfère avec le front d'onde de mesure est plan, mais il peut être incliné par rapport au plan idéal. Cette inclinaison peut être produite par un basculement du miroir
monté sur le transducteur piézoélectrique. A priori, le front réfléchi qui interfère avec le front d'onde de mesure est plan, mais il peut être incliné par rapport au plan idéal. Cette inclinaison peut être produite par un basculement du miroir
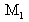 . Le lecteur notera qu'un basculement du miroir
. Le lecteur notera qu'un basculement du miroir
 produit le même effet. Si le miroir
produit le même effet. Si le miroir
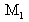 est légèrement translaté par le
est légèrement translaté par le
 le front d'onde de référence subira un déphasage uniforme de tous ses points. On notera
le front d'onde de référence subira un déphasage uniforme de tous ses points. On notera
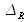 l'écart normal du front d'onde issu du bras de référence (
l'écart normal du front d'onde issu du bras de référence (
 , aller-retour).
, aller-retour).
Dans le bras de mesure, le miroir
 peut être basculé ou translaté longitudinalement. La translation longitudinale du miroir
peut être basculé ou translaté longitudinalement. La translation longitudinale du miroir
 de part et d'autres du foyer paraxial du système optique produira une défocalisation, ce qui se traduira par une contribution du miroir à l'écart normal d'aberration de l'ensemble système optique-miroir
de part et d'autres du foyer paraxial du système optique produira une défocalisation, ce qui se traduira par une contribution du miroir à l'écart normal d'aberration de l'ensemble système optique-miroir
 . On parle également d'un « défaut de mise au point ».
. On parle également d'un « défaut de mise au point ».
Expression générale de l'interférogramme
Supposons que les polarisations des deux bras sont parallèles, l'interférogramme s'écrit :
où :
-
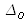 est l'écart normal du front d'onde issu du bras de mesure (système optique+
est l'écart normal du front d'onde issu du bras de mesure (système optique+
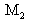 , aller-retour),
, aller-retour),
-
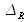 est l'écart normal du front d'onde issu du bras de référence (
est l'écart normal du front d'onde issu du bras de référence (
 , aller-retour),
, aller-retour),
-
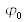 est la phase optique correspondant à la différence de chemin optique totale entre les deux chemins de l'interféromètre, estimée au niveau du capteur d'images.
est la phase optique correspondant à la différence de chemin optique totale entre les deux chemins de l'interféromètre, estimée au niveau du capteur d'images.
En fonction des contributions apportées par les différents éléments, les franges de l'interféromètre auront des formes différentes.
Dans ce qui suit, on suppose
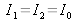 , c'est à dire que les franges ont un contraste maximum, égal à 1.
, c'est à dire que les franges ont un contraste maximum, égal à 1.
Interférogramme avec système optique parfait
Considérons que tout est parfait : système optique, miroir
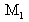 perpendiculaire à l'axe optique et miroir
perpendiculaire à l'axe optique et miroir
 perpendiculaire à l'axe et non défocalisé. Les écarts normaux des contributions sont donc
perpendiculaire à l'axe et non défocalisé. Les écarts normaux des contributions sont donc
 , l'interférogramme est simplement
, l'interférogramme est simplement
Il ne présente pas de franges mais « une teinte plate ».
Comme nous l'avons dit précédemment, un basculement de l'un des miroirs
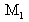 ou
ou
 produira le même effet : un basculement du front d'onde en sortie. Supposons que le basculement soit produit par le miroir
produira le même effet : un basculement du front d'onde en sortie. Supposons que le basculement soit produit par le miroir
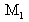 . Ce basculement du front d'onde se traduit en terme d'écart normal par l'équation d'un plan de sorte que :
. Ce basculement du front d'onde se traduit en terme d'écart normal par l'équation d'un plan de sorte que :
où
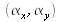 sont les angles de basculement du miroir respectivement dans les directions
sont les angles de basculement du miroir respectivement dans les directions
 . L'interférogramme présente donc des franges rectilignes telles que celles illustrées sur la figure 12.
. L'interférogramme présente donc des franges rectilignes telles que celles illustrées sur la figure 12.
Considérons maintenant que le miroir
 est légèrement défocalisé par une translation
est légèrement défocalisé par une translation
 le long de l'axe optique. L'écart normal généré par cette défocalisation s'écrit [
] :
le long de l'axe optique. L'écart normal généré par cette défocalisation s'écrit [
] :
Les notations sont illustrées sur la figure 24.
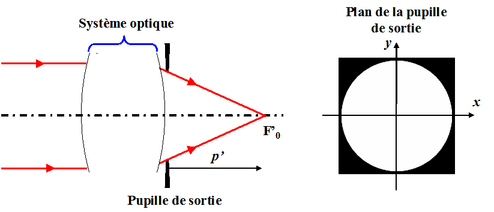
La figure 25 illustre la forme du front d'onde et l'interférogramme obtenu avec la défocalisation du miroir
 .
.
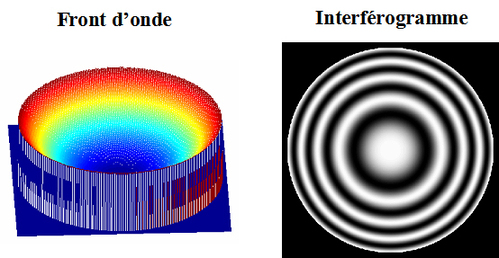
Interférogramme avec aberration sphérique du 3ème ordre
L'aberration sphérique est une aberration d'ouverture, c'est à dire qui apparaît pour l'image d'un point situé sur l'axe optique du système imageur dont le diamètre d'ouverture est grand (ouverture numérique supérieure à 0,35). Dans le cas où le système optique est entaché d'aberration sphérique du 3ème ordre, l'écart normal s'exprime par la relation suivante [ ] :
où
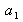 est le coefficient d'aberration sphérique du 3ème ordre.
est le coefficient d'aberration sphérique du 3ème ordre.
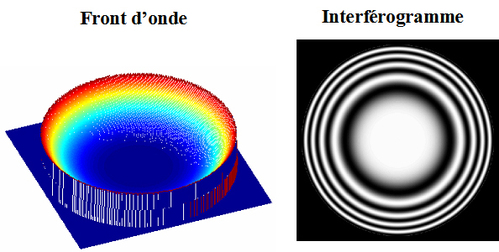
La figure 26 illustre la forme du front d'onde et l'interférogramme en présence d'aberration sphérique du 3ème ordre.
Si maintenant le miroir
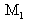 est basculé, la différence des fronts d'onde en sortie de l'interféromètre devient :
est basculé, la différence des fronts d'onde en sortie de l'interféromètre devient :
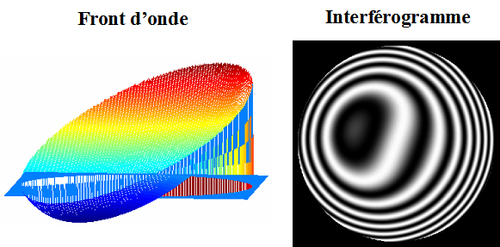
La figure 27 illustre la forme du front d'onde et l'interférogramme en présence d'aberration sphérique du 3ème ordre et d'un basculement du miroir
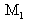 .
.
Dans le cas où le miroir
 est légèrement défocalisé, la différence des fronts d'onde en sortie de l'interféromètre devient :
est légèrement défocalisé, la différence des fronts d'onde en sortie de l'interféromètre devient :
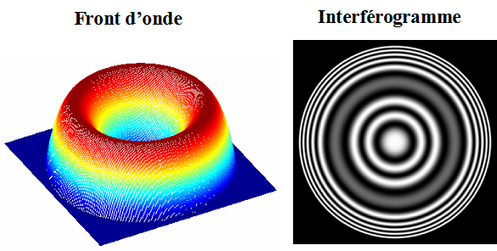
La figure 28 illustre la forme du front d'onde et l'interférogramme en présence d'aberration sphérique du 3ème ordre et d'une défocalisation du miroir
 .
.
Interférogramme avec aberration de coma du 3ème ordre
L'aberration de coma (ou aberration d'aigrette) est une aberration d'ouverture et de champ, c'est à dire qui apparaît hors de l'axe. Dans la configuration présentée figure 22, il n'est pas possible de mettre en évidence la coma. Le montage doit être adapté pour simuler la présence d'une image étendue
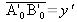 . Pour ce faire il suffit de tourner le système optique d'un angle
. Pour ce faire il suffit de tourner le système optique d'un angle
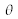 . Ainsi les rayons parallèles à l'axe de l'interféromètre convergent vers le point image
. Ainsi les rayons parallèles à l'axe de l'interféromètre convergent vers le point image
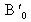 , qui est confondu avec le centre de courbure du miroir
, qui est confondu avec le centre de courbure du miroir
 et le pied de l'image,
et le pied de l'image,
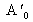 , étant situé au foyer paraxial du système. La taille de l'image est
, étant situé au foyer paraxial du système. La taille de l'image est
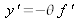 . L'écart normal de coma s'exprime par la relation suivante [
] :
. L'écart normal de coma s'exprime par la relation suivante [
] :
où
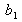 est le coefficient d'aberration de coma du 3ème ordre.
est le coefficient d'aberration de coma du 3ème ordre.
La figure 29 montre la configuration expérimentale pour la mesure de la coma.
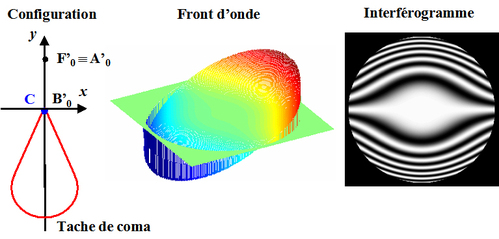
La figure 30 illustre la forme du front d'onde et l'interférogramme en présence d'aberration de coma du 3ème ordre. La configuration initiale correspond au cas où l'image paraxiale est confondue avec le centre de courbure de
 : on peut donc déplacer le centre de courbure dans la tache de coma et étudier l'aberration. Ce déplacement sera effectué par un basculement de
: on peut donc déplacer le centre de courbure dans la tache de coma et étudier l'aberration. Ce déplacement sera effectué par un basculement de
 .
.
Avec un basculement de
 pour mettre
pour mettre
 en dehors de la tache de coma, le front d'onde d'aberration devient :
en dehors de la tache de coma, le front d'onde d'aberration devient :
La figure 31 illustre ce cas.
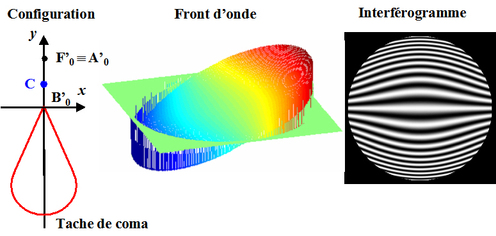
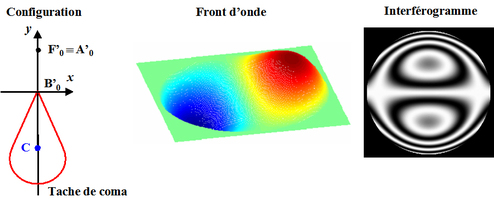
La figure 32 montre l'écart normal et l'interférogramme obtenu lorsque
 est à l'intérieur de la tache de coma.
est à l'intérieur de la tache de coma.
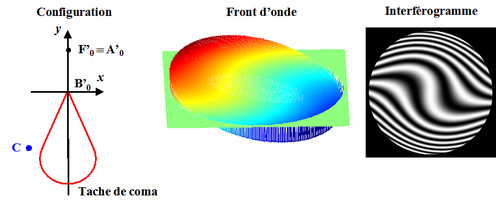
La figure 33 montre l'écart normal et l'interférogramme obtenu lorsque
 est déplacé hors du plan méridien et hors de la tache de coma.
est déplacé hors du plan méridien et hors de la tache de coma.
Interférogramme avec aberration d'astigmatisme du 3ème ordre
L'aberration d'astigmatisme est également une aberration d'ouverture et de champ, c'est à dire qui apparaît pour le point hors de l'axe. L'écart normal d'astigmatisme s'exprime par la relation suivante [ ] :
où
 et
et
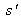 sont les positions des foyers tangentiel et sagittal par rapport au plan focal paraxial.
sont les positions des foyers tangentiel et sagittal par rapport au plan focal paraxial.
La figure 34 illustre la forme du front d'onde et l'interférogramme en présence d'astigmatisme du 3ème ordre, lorsque le centre de courbure du miroir est confondu avec l'image paraxiale
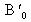 .
.
Dans le cas où on défocalise le miroir sphérique
 , l'écart normal devient :
, l'écart normal devient :
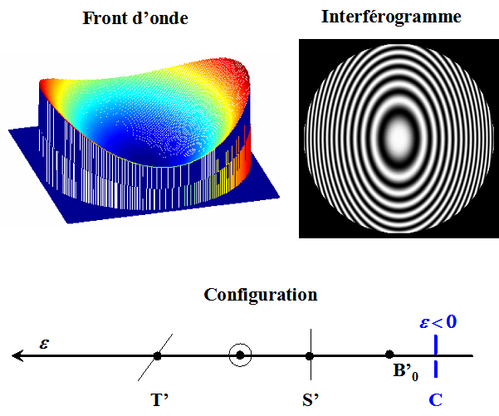
Pour
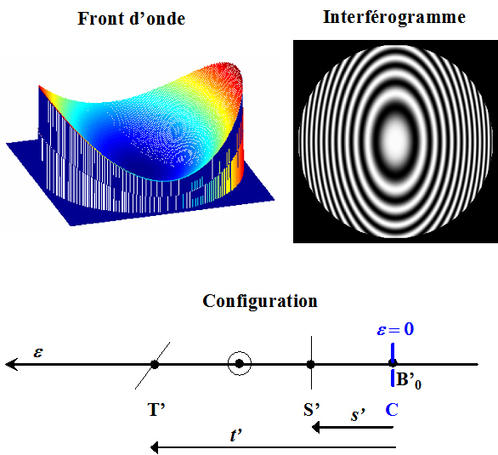
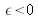 , le centre de courbure est au delà de l'image paraxiale, la surface d'onde est torique et les franges sont des ellipses, comme l'illustre la figure 35.
, le centre de courbure est au delà de l'image paraxiale, la surface d'onde est torique et les franges sont des ellipses, comme l'illustre la figure 35.
Lorsque
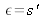 , la surface d'onde est cylindrique d'axe vertical et les franges sont rectilignes et verticales, le centre de courbure du miroir
, la surface d'onde est cylindrique d'axe vertical et les franges sont rectilignes et verticales, le centre de courbure du miroir
 est alors sur la focale sagittale (figure 36).
est alors sur la focale sagittale (figure 36).
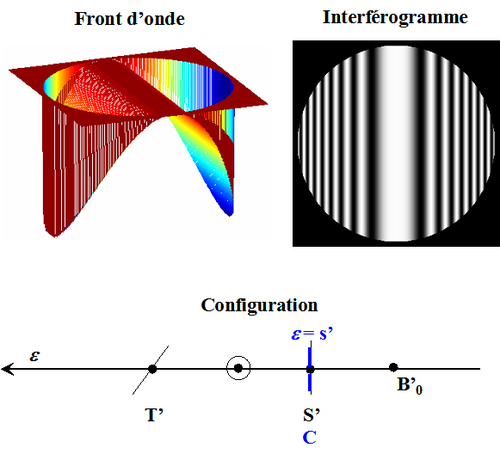
Lorsque
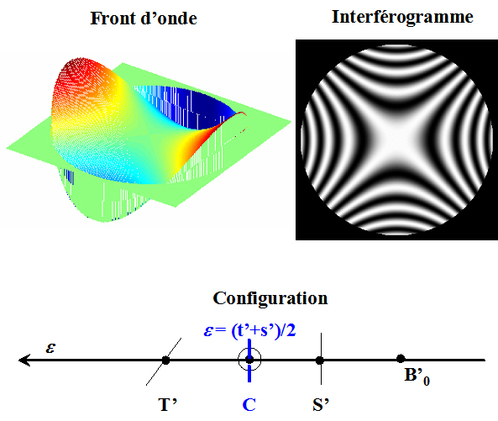
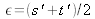 , la surface d'onde est un tore en diabolo et les franges sont en forme de croix, le centre de courbure du miroir
, la surface d'onde est un tore en diabolo et les franges sont en forme de croix, le centre de courbure du miroir
 est alors sur le cercle de moindre diffusion situé à mi distance des focales sagittale et tangentielle (figure 37).
est alors sur le cercle de moindre diffusion situé à mi distance des focales sagittale et tangentielle (figure 37).
Lorsque
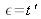 , la surface d'onde est à nouveau cylindrique mais d'axe horizontal et les franges sont rectilignes et horizontales, le centre de courbure du miroir
, la surface d'onde est à nouveau cylindrique mais d'axe horizontal et les franges sont rectilignes et horizontales, le centre de courbure du miroir
 est alors sur la focale tangentielle (figure 38).
est alors sur la focale tangentielle (figure 38).
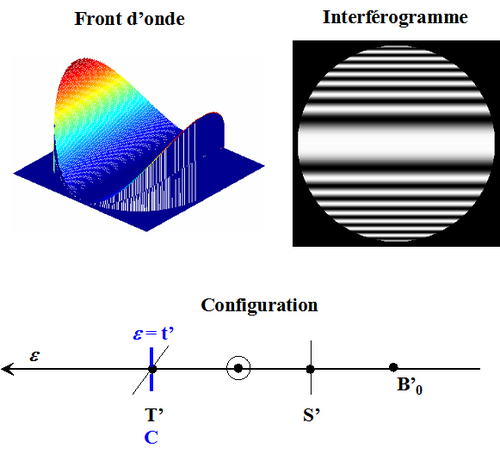
Enfin, lorsque
 , le centre de courbure du miroir est entre le système optique et la focale tangentielle, la surface d'onde est à nouveau torique et les franges sont elliptiques avec un grand axe horizontal (figure 39).
, le centre de courbure du miroir est entre le système optique et la focale tangentielle, la surface d'onde est à nouveau torique et les franges sont elliptiques avec un grand axe horizontal (figure 39).
