
Spectrométrie par transformée de Fourier
Une application des interféromètres concerne la spectrométrie par transformée de Fourier. La spectrométrie est la mesure du spectre d'un rayonnement. Comme nous l'avons vu dans le cours « Interférences : Fondamentaux », la cohérence de la source lumineuse, donc son spectre, influence fortement l'interférogramme observé lorsque l'on fait varier la différence de chemin optique. La spectrométrie par transformée de Fourier est une application directe du théorème de Wiener–Khintchine. D'après le cours « Interférences : Fondamentaux », l'interférogramme s'écrit
où
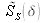 est la transformée de Fourier de la densité spectrale d'énergie de la source,
est la transformée de Fourier de la densité spectrale d'énergie de la source,
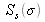 , et
, et
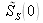 est la valeur de
est la valeur de
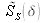 pour
pour
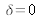 .
.
Comme l'interférogramme s'écrit aussi sous la forme
La transformée de Fourier inverse de
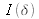 devient
devient
La transformée de Fourier est une fonction trimodale dont la partie des
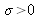 est proportionnelle au spectre de la source. Pratiquement, on enregistre l'interférogramme sur une différence de marche totale
est proportionnelle au spectre de la source. Pratiquement, on enregistre l'interférogramme sur une différence de marche totale
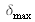 et le signal est numérisé sur
et le signal est numérisé sur
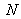 points d'échantillonnage, ensuite on calcule le spectre par une transformée de Fourier discrète (algorithmes FFT). La résolution spectrale atteignable avec cette technique dépend de la fonction de filtrage de la transformée de Fourier discrète.
points d'échantillonnage, ensuite on calcule le spectre par une transformée de Fourier discrète (algorithmes FFT). La résolution spectrale atteignable avec cette technique dépend de la fonction de filtrage de la transformée de Fourier discrète.
Notons
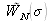 cette fonction, on a [] :
cette fonction, on a [] :
La fonction
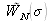 est la fonction de raie dans le spectre calculé par FFT. La largeur de la fonction de raie est donnée par
est la fonction de raie dans le spectre calculé par FFT. La largeur de la fonction de raie est donnée par
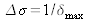 . Ainsi le pouvoir de résolution du spectromètre est donné par
. Ainsi le pouvoir de résolution du spectromètre est donné par
Le pouvoir de résolution dépend donc du rapport entre la différence de chemin optique enregistrée et la longueur d'onde moyenne de la source : il est égal au nombre de franges enregistrées.
Un dispositif expérimental permettant d'appliquer cette technique est décrit figure 40.
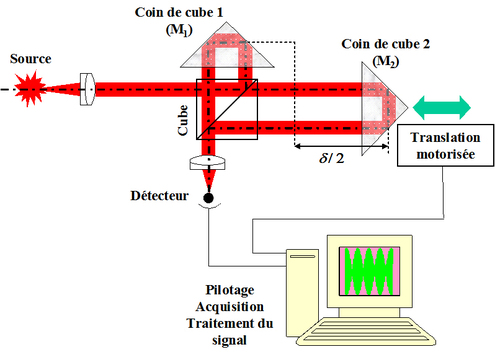
Les miroirs plans du Michelson classique sont remplacés par deux coins de cube qui ont la particularité de renvoyer la lumière dans la direction opposée. Le coin de cube n°2 est monté sur une platine de translation pilotée par l'ordinateur. Pour un déplacement du cube de
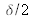 , on produit une différence de chemin optique de
, on produit une différence de chemin optique de
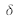 . L'utilisation de coins de cube permet de translater le cube-miroir sans avoir à le ré-aligner à chaque translation. L'acquisition du signal par le détecteur est pilotée par le PC de façon synchrone avec la translation du cube.
. L'utilisation de coins de cube permet de translater le cube-miroir sans avoir à le ré-aligner à chaque translation. L'acquisition du signal par le détecteur est pilotée par le PC de façon synchrone avec la translation du cube.
A titre d'illustration, la figure 41 montre l'interférogramme obtenu avec une lampe à vapeur de sodium basse pression.
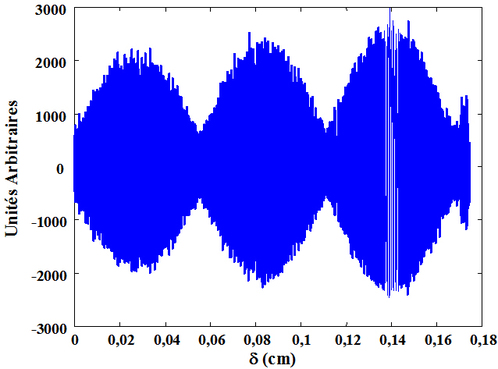
Le calcul du spectre par FFT donne le résultat de la figure 42. On observe bien la symétrie du spectre.
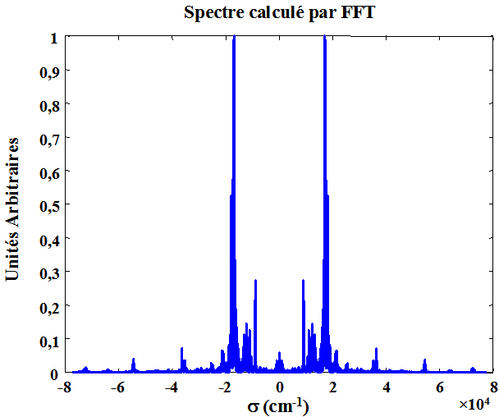
Après extraction de la partie des nombres d'ondes positifs, le spectre de la source en fonction du nombre d'onde et de la longueur d'onde est donné sur la figure 43.
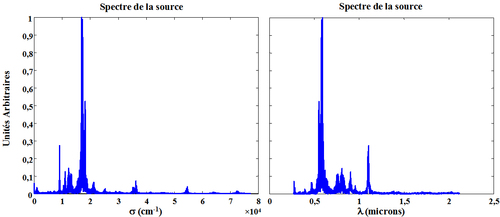
Une seconde illustration concerne une lampe à incandescence, dont l'interférogramme mesuré est donné sur la figure 44.
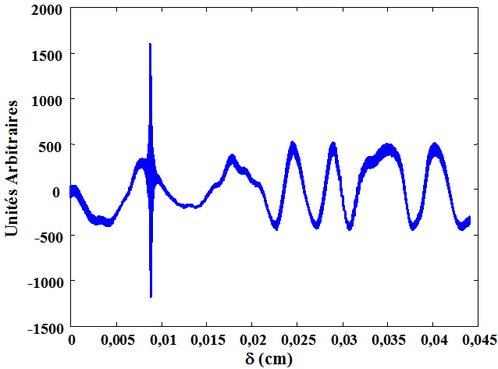
Après calcul numérique, le spectre de la source en fonction de la longueur d'onde est représenté sur la figure 45.
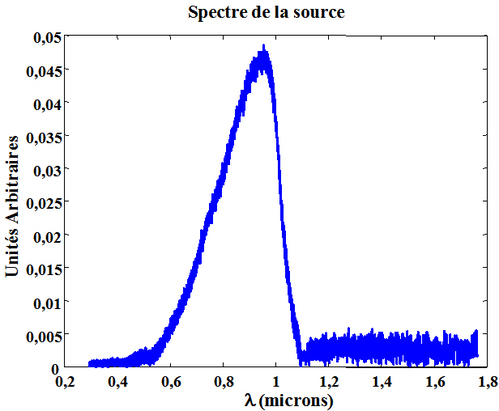
Ce dernier résultat appelle un commentaire issu de l'observation du spectre en fonction de la longueur d'onde. La lampe à incandescence est une source de type corps noir dont la bande spectrale est très large et couvre de l'UV jusqu'à l'IR. Or le résultat de la figure 45 montre que le spectre s'atténue brutalement vers
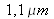 . Ceci est du à la bande spectrale de sensibilité du détecteur à base de silicium qui coupe à cette longueur d'onde, et qui est utilisé dans le dispositif de la figure 40. On constate ainsi que le spectre mesuré est influencé par la sensibilité spectrale du capteur. En toute rigueur il faut corriger la mesure et traiter le spectre en le divisant par la sensibilité du capteur pour toutes les longueurs d'ondes mesurables. Ce traitement n'a pas été appliqué pour les résultats présentés dans cette étude de cas.
. Ceci est du à la bande spectrale de sensibilité du détecteur à base de silicium qui coupe à cette longueur d'onde, et qui est utilisé dans le dispositif de la figure 40. On constate ainsi que le spectre mesuré est influencé par la sensibilité spectrale du capteur. En toute rigueur il faut corriger la mesure et traiter le spectre en le divisant par la sensibilité du capteur pour toutes les longueurs d'ondes mesurables. Ce traitement n'a pas été appliqué pour les résultats présentés dans cette étude de cas.