Spectromètre de Fabry-Pérot

L'interféromètre à ondes multiples de Fabry-Pérot peut être utilisé comme un spectromètre. La configuration expérimentale est décrite figure 46. Le Fabry-Pérot est de type confocal : les miroirs sont sphériques de mêmes rayons de courbure et leurs foyers sont confondus, la cavité est stable de sorte que la lumière peut effectuer une infinité d'aller-retours en restant confinée au voisinage de l'axe optique.

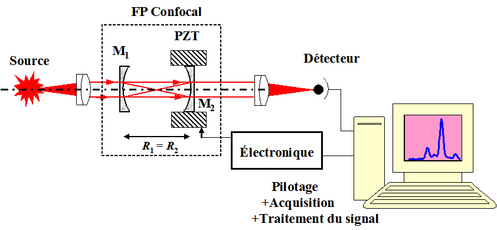
L'un des miroirs est monté sur un transducteur piézoélectrique qui permet de faire varier l'épaisseur de la cavité et d'effectuer un balayage spectral. La tension de pilotage du PZT est une rampe et pour chaque fréquence du spectre en phase avec la longueur instantanée de la cavité l'intensité lumineuse sur le détecteur est maximale.

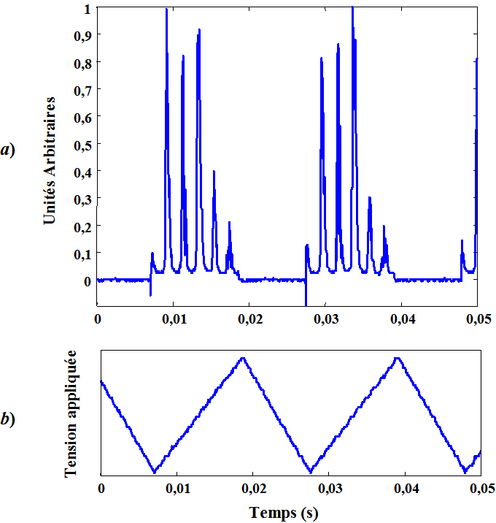
A titre d'illustration, la figure 47 illustre le principe dans la cas d'un laser HeNe multimodes. La figure 47b montre la rampe de tension qui pilote le PZT et en figure 47a on observe le spectre du laser.

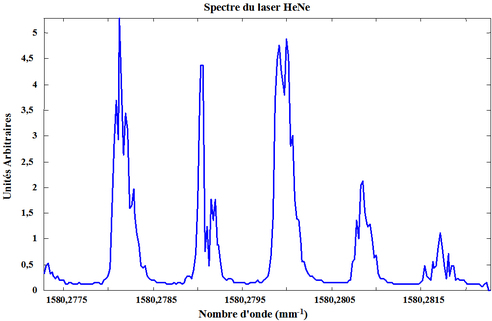
La figure 48 correspond à une période du signal observé en figure 47a. L'axe horizontal est donné en nombre d'onde par correspondance entre l'échelle temporelle et l'échelle fréquentielle. En effet, une période du signal de la figure 47 correspond à l'intervalle spectral libre du Fabry-Pérot.

Les caractéristiques du spectromètre présenté ici sont les suivantes :

• intervalle spectrale libre 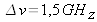soit

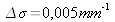
• finesse

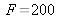
• résolution instrumentale 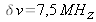soit

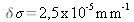
• échantillonnage numérique 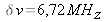soit

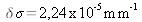
Comme l'épaisseur de la cavité d'air constituée par les deux miroirs est 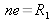, le pouvoir de résolution du spectromètre est donné par (voir figure 18 pour les notations)

Il est proportionnel à la finesse de l'interféromètre et dépend de la longueur d'onde moyenne analysée.

D'après le cours « Interférences : fondamentaux », le degré de cohérence est donné par :

où est la transformée de Fourier de , enveloppe spectrale du rayonnement.

La longueur de cohérence de la source peut être estimée par :

Considérant que la mesure du spectre par le Fabry-Pérot donne accès directement à la quantité , le degré de cohérence est calculé par une transformée de Fourier discrète du spectre mesuré. La figure 49 montre le degré de cohérence du laser HeNe calculé à partir du résultat de la figure 48.

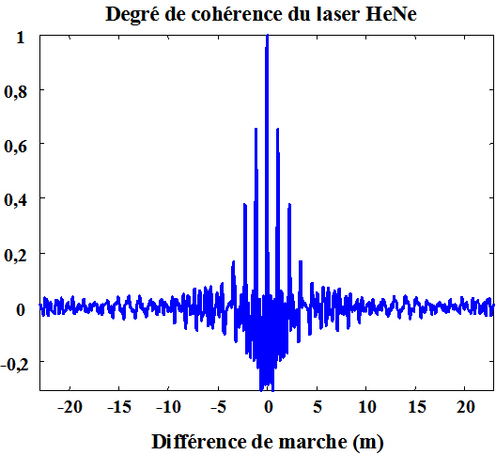
La longueur de cohérence calculée numériquement à partir du degré de cohérence est estimée égale à .

Une seconde illustration concerne une diode laser à 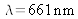dont le spectre mesuré par l'interféromètre est illustré sur la figure 50.

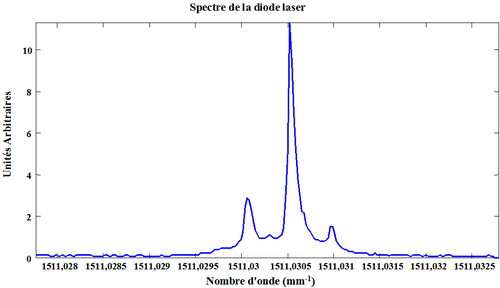
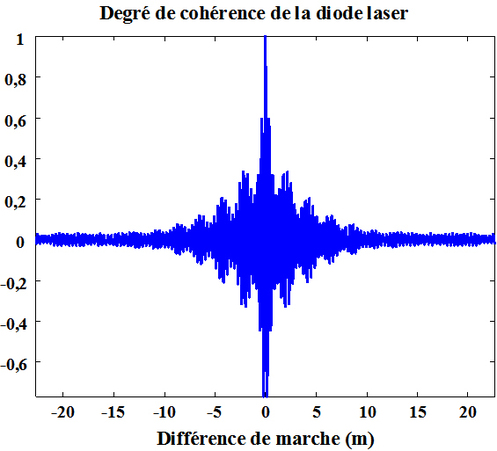
Le degré de cohérence de la diode laser est calculé par FFT et il est représenté sur la figure 51. Sa longueur de cohérence est estimée égale à .