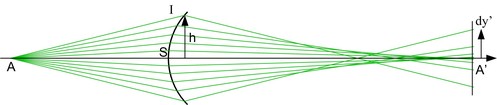
Image d'un point lumineux dans un dioptre

Considérons un dioptre sphérique séparant deux milieux d'indices n et n', défini par son centre de courbure C, son sommet S, son rayon de courbure .

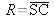Toutes les longueurs et les angles sont orientés en utilisant la convention de la trigonométrie.

Un point A est situé dans l'espace objet sur la droite SC. Le rayon issu de A passant par S est perpendiculaire au dioptre, il n'est pas dévié. Un autre rayon issu de A passant par un point quelconque I du dioptre subit une réfraction le rayon émergent coupe SC en un point A'.

Cherchons la position de A'. Suivant la figure  12 :

Figure 12 [zoom...]

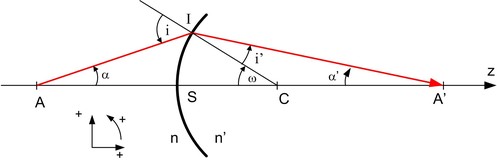
i est l'angle d'incidence du rayon sur le dioptre

i' est l'angle de réfraction, et, d'après (5), n.sin(i) = n'.sin(i')

Une formule classique dans le triangle CAI donne :

On peut écrire aussi :

et donc :

Le stigmatisme de la conjugaison voudrait que A' ne dépende pas de la position de I. Il faut alors que CA' reste fixe de même que le rapport IA/IA'. Ceci n'est obtenu que dans une position particulière de A et n'est pas réalisé dans le cas général.

La figure 13 montre concrètement un exemple de tracé de rayon dans un dioptre, l'aberration y est importante. Ce tracé est obtenu avec le logiciel gratuit Oslo-Edu téléchargeable à l'adresse : http://www.lambdares.com/downloads/index.phtml#osloedu

Figure 13 [zoom...]