Optique géométrique : Fondamentaux
Miroirs sphériques
Un miroir sphérique est une surface réfléchissante concave ou convexe définie par son centre de courbure C et un sommet S situé sur la surface. Le rayon de courbure est
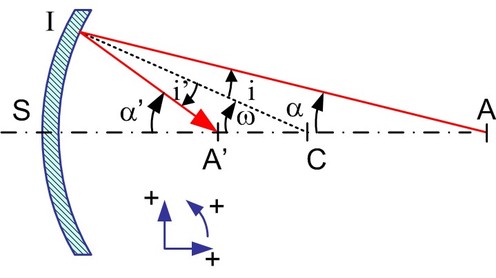
Figure 25
[zoom...]
![[zoom...]](javascript:window.open(%22../res/fig23_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
Considérons un point A de la droite SC. Un rayon lumineux issu de A se réfléchit en un point I du miroir et coupe la droite SC en A'. En effectuant le même calcul et le même raisonnement que pour les dioptres, nous avons :
et
or sin(i) = - sin(i ') donc :
L'expression ci-dessus est analogue à celle des dioptres (7) en remplaçant n' par –n. Nous avons donc, comme pour le dioptre,
:
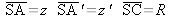inchangé
toujours négatif
Ces formules sont identiques que le miroir soit concave ou convexe.
La formule de conjugaison est symétrique en
et
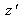. Si A' est image de A, A est image de A'.