Cohérence de l'éclairage et limite de résolution

Le phénomène de diffraction impose une limite physique de l'ordre de la longueur d'onde à la taille des objets que l'on peut résoudre avec un système optique comme un microscope. Pour déterminer quantitativement l'importance de la dégradation de l'image imposée par la diffraction, il est intéressant de passer dans l'espace des fréquences spatiales de l'objet observé et de raisonner sur la fonction de transfert de modulation (FTM) du système. (Voir le cours de Formation des images dans le module d'Optique de Fourier, ou les références [ ], [ ] ). La théorie montre que la dégradation de l'image ne dépend pas seulement des propriétés de l'objectif (ouverture numérique, aberrations) mais dépend également de la cohérence spatiale de l'éclairage, propriété directement reliée à l'ouverture numérique de ce dernier.

Lorsque le diaphragme d'ouverture est très fermé (source quasi-ponctuelle), l'objet est éclairé par une onde quasi-plane, et l'éclairage est dit spatialement cohérent. Le formalisme de Fourier s'applique alors sur les amplitudes complexes des ondes. 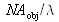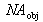Un système optique sans aberration (limité par la diffraction) est dans ce cas un filtre passe-bas des fréquences spatiales qui laissent passer sans altération les fréquences inférieures à où représente l'ouverture numérique objet de l'objectif et coupe strictement les fréquences supérieures (cf. Fig. 10, courbe 1). Dans ces conditions les images sont bien contrastées mais les éléments de l'image sont entourés de franges liées au phénomène de Gibbs.

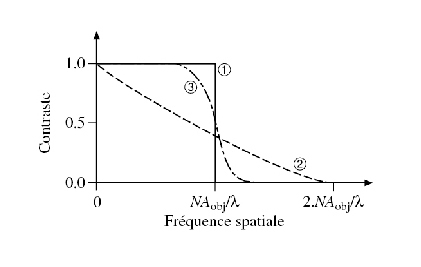
Inversement, si le diaphragme d'ouverture est très ouvert afin de rendre l'ouverture numérique de l'éclairage supérieure à celle de l'objectif, l'éclairage est dit totalement incohérent. Le formalisme de Fourier s'applique alors à la puissance surfacique de l'onde (module carré de l'amplitude complexe). Un système optique sans aberration est alors un filtre passe-bas dont la fonction de transfert décroît graduellement de 1 à 0 lorsque la fréquence croît de la valeur nulle à 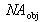(cf. Fig. 10, courbe 2). La fréquence de coupure est donc deux fois supérieure à celle obtenue en éclairage cohérent. Cependant, le contraste d'un objet périodique est d'autant plus affaibli par le système optique que sa fréquence spatiale est élevée.

Dans les cas intermédiaires, l'éclairage est dit partiellement cohérent (Voir la référence [ ] ). Il n'est dans ce cas plus possible de définir en toute rigueur une fonction de transfert, le système ne relevant plus de la théorie des systèmes linéaires. On peut cependant avoir une bonne idée de l'effet du système optique sur l'image en déterminant le contraste d'une mire sinusoïdale en fonction de la fréquence spatiale (Cf. Fig. 10, courbe 3). 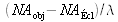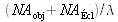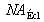On peut remarquer que le contraste reste à 1 pour toutes les fréquences inférieures à puis décroît graduellement pour atteindre 0 à la fréquence où est l'ouverture numérique de l'éclairage déterminée par le réglage du diaphragme d'ouverture du condenseur ; la référence [ ] expose une démonstration astucieuse de cette propriété. Les observations microscopiques se font presque toujours dans ces conditions d'éclairage. Elles donnent en effet une image qui contient des hautes fréquences spatiales et dont les éléments de basses et moyennes fréquences spatiales sont très bien contrastés ce qui satisfait le sens subjectif de la vision de l'observateur. La valeur optimale de l'ouverture numérique de l'éclairage, à ajuster pour chaque objet (et observateur), est empiriquement de l'ordre des deux tiers de celle de l'objectif.

Pour vérifier l'influence de la cohérence de l'éclairage sur la formation des images, il est intéressant d'utiliser des préparations de diatomées tests. Les diatomées forment une famille très vaste et diverse d'animaux aquatiques microscopiques aux squelettes constitués de structures périodiques très fines dont les dimensions des motifs s'échelonnent de ~2 µm à ~0,25 µm suivant les espèces. Ces 'objets' sont donc particulièrement bien adaptés pour mettre en évidence de manière directe la limite de résolution des objectifs de microscope.