Rappels sur le filtrage des fréquences spatiales

Seules les grandes lignes des méthodes de filtrage des fréquences spatiales utilisées en microscopie seront rappelées ici. Le lecteur est supposé préalablement connaître le principe du filtrage des fréquences spatiales et le montage classique de double diffraction . Pour tout renseignement sur les fondements et les détails de cette méthode nous renvoyons le lecteur au grain " Formation des images " et aux références [ ou ].

La théorie, qui relève du filtrage linéaire sur l'amplitude complexe, sera présentée en supposant l'éclairage monochromatique et spatialement cohérent. On rappelle toutefois que l'œil ou les détecteurs usuels sont sensibles à l'éclairement, proportionnel au module carré de l'amplitude complexe.

Pour passer au cas des observations usuelles en microscopie, faites en lumière blanche , il suffit de réaliser que l'observation globale sera simplement la superposition incohérente (i.e. en éclairement), des différentes images monochromatiques obtenues par le filtrage ; la propriété d'amélioration du contraste des objets est donc naturellement conservée en lumière polychromatique. Quelques commentaires seront faits dans certains cas sur les aspects de cohérence spatiale.

Soit une préparation microscopique formant un objet mince caractérisé par sa transmittance complexe t(M) où M représente un point du plan de la préparation.

Cet objet est éclairé par une onde plane provenant de l'éclairage Köhler en condition d'éclairage spatialement cohérent, c'est à dire avec un diaphragme d'ouverture quasi-ponctuel. Voir Fig.8 (Revoir le grain "Principes et utilisations de base du microscope" en ce qui concerne la description de l'éclairage Köhler).

Dans le plan de Fourier, qui correspond en microscopie au plan focal image de l'objectif du microscope (confondu avec le plan de la pupille de sortie de cet objectif), on obtient, à une homothétie et un facteur de phase près, une amplitude complexe proportionnelle à la transformée de Fourier de t :

Dans le cas qui nous intéresse ici, l'objet est usuellement un pur objet de phase, c'est à dire :

où  est une fonction à valeur réelle représentant le déphasage introduit par l'objet en chaque point de celui-ci. La phase globale de l'onde étant sans importance, on choisit de telle sorte que sa valeur moyenne soit nulle. Si les variations de phase sont faibles ( ), l'exponentielle peut être approchée par son développement limité (au premier ordre) et on obtient pour l'amplitude complexe au niveau de l'objet :

Soit au niveau du plan de Fourier :

où 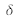 est la distribution de Dirac, et la transformée de Fourier de . Cela signifie en pratique que l'on a un point très lumineux au centre du plan de Fourier ( 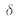) et de la lumière diffractée dans tout le plan ( ).

Pour le montage de double diffraction, sans filtrage dans le plan de Fourier, on a donc :

où  (Le renversement de l'image induit par la double TF du montage de double diffraction exprime simplement la conjugaison d'optique géométrique avec un grandissement négatif). L'éclairement perçu par l'œil est proportionnel à qui vaut donc 1 pour un calcul au premier ordre, le terme d'ordre 2 étant non significatif ( , est négligeable devant 1) ; un pur objet de phase est vu comme une plage uniformément éclairée.

En fait ce résultat n'est pas tout à fait exact car l'ouverture numérique finie de l'objectif conduit à une extension limitée de la lumière dans le plan de Fourier (cette limite correspond à la pupille de sortie de l'objectif). L'amplitude complexe de l'image finale est donc l'amplitude complexe de l'objet convolué par la réponse percutionnelle cohérente de l'objectif (l'amplitude complexe de la tache d'Airy si l'objectif est “limité par la diffraction”). L'image peut par conséquent présenter quelques variations du module de l'amplitude complexe (phénomène de Gibbs dû à la coupure brutale des hautes fréquences spatiales, matérialisé par la présence de franges au niveau des changements rapides de phase de l'objet). Cf. Figure 7b.