Évaluation de Type B
Si un laboratoire de mesure disposait de ressources et d'un temps illimités, il pourrait effectuer une recherche statistique exhaustive de toutes les causes imaginables d'incertitude, en utilisant par exemple des instruments de différents types et de différents fabricants, avec différentes méthodes de mesure, différents modes opératoires et différentes approximations dans les modèles théoriques du mesurage.
Les incertitudes associées à toutes ces causes pourraient être alors évaluées par l'analyse statistique de séries d'observations et l'incertitude due à chaque cause pourrait être caractérisée par un écart-type évalué statistiquement. Finalement, toutes les composantes de l'incertitude seraient obtenues par des évaluations de Type A.
Comme une telle étude n'est pas envisageable économiquement, de nombreuses composantes de l'incertitude doivent être évaluées par tous les autres moyens praticables. L'ensemble des informations recherchées peut comprendre :
-
des résultats de mesures antérieures,
-
la connaissance générale ou empirique du comportement des instruments utilisés,
-
les spécifications du fabricant,
-
les certificats d'étalonnage,
-
l'incertitude attribuée à des valeurs de référence provenant d'ouvrages, manuels et autres normes.
Ainsi pour une estimation xi d'une grandeur Xi. qui n'a pas été obtenue à partir d'observations répétées, la variance estimée u2(xi) ou l'incertitude-type u(xi) est évaluée par un jugement scientifique fondé sur toutes les informations disponibles à propos de la variabilité possible de Xi . L'incertitude-type ainsi évaluée est appelée incertitude-type de Type B.
En pratique, il est notamment nécessaire de faire un bilan des erreurs que l'on répartit en :
-
Erreurs systématiques (cf. VIM §3.14) telles que l'erreur de parallaxe lors de la lecture sur un cadran à aiguille, le réglage de zéro d'un appareil, les erreurs de méthode, le vieillissement des composants, ...
-
Erreurs aléatoires (cf. VIM §3.13) telles que les erreurs de lecture ou dues à l'appareil lui-même, ou dues aux conditions extérieures (température, dilatation thermique, pression atmosphérique, humidité, ...).
Lois de probabilité à priori
Pour arriver à exprimer l'incertitude de Type B sous forme d'un écart-type, il faut recourir à des lois de probabilité dont les plus employées sont rassemblées dans le tableau 2. À noter qu'elles se rapportent içi à une distribution de valeurs d'une variable aléatoire de moyenne µ=0 et d'étendue
![[zoom...]](javascript:window.open(%22../res/tablo_02_1.png%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
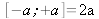
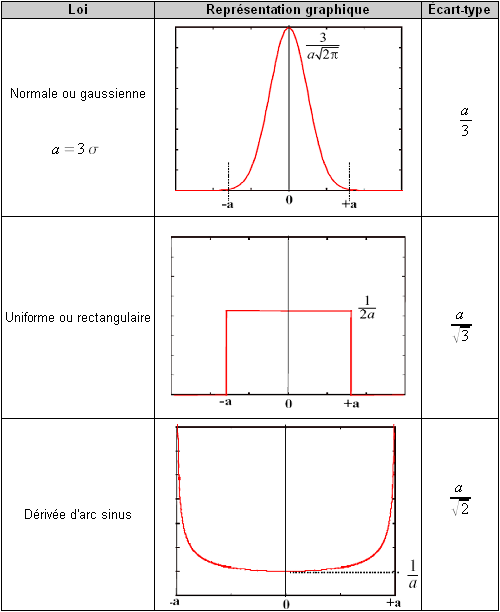
D'une manière générale, si le constructeur fournit l'incertitude-type, on l'utilise directement.
Si on a très peu d'information sur une grandeur d'entrée et que l'intervalle de variation supposé de celle-ci est de la forme :
-
alors l'incertitude-type est :
-
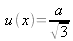
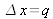alors l'incertitude-type est :
en considérant une loi uniforme sur l'intervalle de variation de la grandeur.
Exemples d'incertitudes de Type B
-
Résolution d'un appareil de mesure
La graduation d'un instrument de mesure analogique ou l'afficheur d'un appareil numérique sont des sources d'incertitude. Si la résolution du dispositif de lecture est δx, la valeur du signal d'entrée qui produit une indication donnée X peut se situer avec une égale probabilité à n'importe quel endroit de l'intervalle
, le signal d'entrée est alors décrit par une loi de probabilité rectangulaire de largeur δx
et d'écart-type
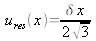appelée incertitude de résolution.
-
Classe d'un instrument
L'Erreur Maximale Tolérée (EMT ; cf. VIM §5.21) donne les limites extrêmes de variation de l'indication obtenue d'un instrument de mesure de classe définie par l'intervalle
. L'incertitude-type associée est alors
.
-
Hystérésis
L'indication d'un instrument peut différer d'une quantité fixe selon que les lectures successives se font par valeurs croissantes ou décroissantes. La plupart du temps le sens de l'hystérésis n'est pas observable. Si la largeur de l'étendue des lectures possibles dues à cette cause est δx, l'incertitude-type due à l'hystérésis est
.
-
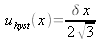Variations de température
Une des principales grandeurs d'influence d'un système de mesure est la température d'environnement du moyen de mesure (local, enceinte climatisée, boîtier, ...). Dans la mesure où la température varierait entre 2 extrema de façon quasi sinusoïdale, la loi de probabilité associée à cette grandeur d'influence est la fonction dérivée d'arc sinus. Si les variations de la température sont telles que
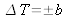alors l'incertitude-type due aux variations de température est
.