Grandeur Y mesurée indirectement
Pour un mesurande Y fonction de plusieurs grandeurs d'entrée Xi
suivant le modèle mathématique du mesurage
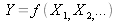, l'incertitude-type de y est obtenue par composition des incertitudes-types des estimations d'entrée xi. Cette incertitude-type
composée de l'estimation y est notée uc(y).
Dans la mesure où la fonction ƒ ne présente pas de non-linéarité importante, on développe celle-ci autour des espérances mathématiques E(xi)=µi des grandeurs d'entrée xi. Le développement en série de Taylor au premier ordre donne, pour des petites variations de y autour de µy :
Le carré de la différence y-µy est alors donné par :
qui peut être écrit sous la forme
L'espérance mathématique de
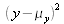est la variance de y, soit
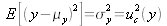d'où finalement :
où
u( x i ) = incertitude-type sur x i
rij = coefficient de corrélation de xi et x j
Cette équation est appelée loi de propagation des incertitudes. Elle montre comment se composent les incertitudes u( xi ) des grandeurs d'entrée xi pour donner l'incertitude uc(y) de la grandeur de sortie y.
Les dérivées partielles
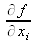sont appelées coefficients de sensibilité. Elles décrivent comment varie l'estimation de sortie y en fonction des variations dans les valeurs des estimations d'entrée
x1, x2,...xp
.
Le coefficient de corrélation rij
est tel que
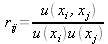où
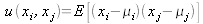est la covariance de
xi
et
x
.j
Grandeurs d'entrée non corrélées
Lorsque toutes les grandeurs d'entrée X1, X2, ...., Xp sont indépendantes, c'est à dire lorsque les covariance u(xi, xj) et les coefficients de corrélation rij sont nuls, l'incertitude-type composée est telle que :
Cas où Y est une somme ou une différence
Soit la grandeur distance L dépendant des grandeurs mesurées position, x1 et position x2 telles que
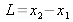. Alors
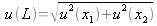. Si
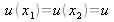alors
.
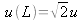Cas où Y est un produit ou un quotient
Soit la grandeur éclairement E dépendant des grandeurs connues ou mesurées intensité IL et distance D. La loi de Bouguer donne
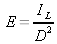soit :
Grandeurs d'entrée corrélées
Si on utilise dans l'estimation des valeurs de grandeurs d'entrée un même étalon physique, un même instrument de mesure, une même donnée de référence ou encore la même méthode de mesure, il existera une corrélation entre grandeurs d'entrée.
De façon générale, si deux grandeurs d'entrée X1
et X2
estimées par
x
1
et
x
2
dépendent d'un ensemble de variables non corrélées Q1, Q
2, ..., QL telles que
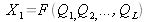et ,
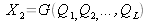la covariance associée à x1 et x
2 est donnée par :
avec u2(q1) la variance associée à l'estimation q1 de Q1.
Le coefficient de corrélation estimé r(x1,x2) est déterminé à partir de l'expression
avec
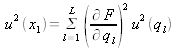et une expression analogue pour u2(
x2
).
Dix résistances électriques, chacune de valeur nominale Ri=1000Ω sont étalonnées par comparaison à une même résistance étalon Rs=1000Ω caractérisée par une incertitude-type u(Rs)=100mΩ.
L'étalonnage de chaque résistance peut être représenté par le modèle mathématique
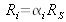avec l'incertitude-type
sur le rapport mesuré
obtenue à partir d'observations répétées. On suppose que
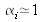pour chaque résistance et que
est à peu près identique pour chaque étalonnage de sorte que
.
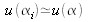Les dix résistances Ri dépendent toutes d'une même variable Rs du fait de leur étalonnage. La covariance associée à Ri et Rj est
et
soit
cela entraîne que le coefficient de corrélation de deux résistances quelconques (i≠j) est
Les valeurs estimées des résistances sont donc corrélées avec un degré de corrélation qui dépend du rapport entre l'incertitude de la comparaison
et l'incertitude de l'étalon de référence u(Rs). Lorsque l'incertitude de comparaison est négligeable par rapport à l'incertitude de l'étalon, les coefficients de corrélation rij
sont égaux à +1 et l'incertitude de chaque résistance étalonnée u(Ri) est la même que celle de l'étalon.
De même que la variance estimée associée à une grandeur d'entrée comporte une composante statistique (Type A) et une composante évaluée (Type B), la covariance estimée associée à deux grandeurs d'entrée peut aussi être composée de deux contributions de Type A et B. Ainsi la covariance estimée de deux grandeurs X et Z qui sont elles-mêmes estimées par les moyennes
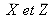déterminées à partir de N paires (x1,zi) indépendantes d'observations simultanées répétées est donnée par
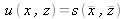avec
Le coefficient de corrélation estimé entre les deux grandeurs X et Z est alors
Si la fréquence d'un oscillateur ne disposant pas de compensation de température est une grandeur d'entrée et que la température ambiante est aussi une grandeur d'entrée et que ces deux grandeurs sont observées simultanément, alors il peut y avoir une corrélation significative mise en évidence par la covariance calculée de la fréquence de l'oscillateur et de la température ambiante.