Système colorimétrique RGB et CIE XYZ

Du fait de la trivariance visuelle, le repérage d'une couleur peut se faire par un ensemble de trois paramètres associés à un point représentatif dans un espace vectoriel à trois dimensions. Plus précisément, une couleur peut être représentée par un vecteur dont le module correspond au niveau lumineux et l'orientation à la chromaticité (cf figure 10).

Dans l'exemple d'espace vectoriel tridimensionnel représenté en figure 10, une couleur quelconque est définie par un vecteur dont les composantes , et (appelées composantes trichromatiques) sont comptées sur chacun des trois axes non coplanaires d'un système de coordonnées ayant pour origine O. Les vecteurs unitaires , et représentent des couleurs primaires non métamères deux à deux et on peut écrire (1)

L'équation (1) signifie que la couleur est égalisée par un mélange des trois couleurs primaires , et .

Par ailleurs, on peut considérer tout rayonnement lumineux comme résultant de la synthèse additive d'un grand nombre de rayonnements s'étendant chacun sur un domaine de longueur d'onde avec une fonction de pondération représentant le spectre de la source de lumière échantillonné à l'aide de la fonction , de telle sorte que :

Si l'intervalle , on voit qu'avec un nombre infini de longueurs d'onde, on peut synthétiser une lumière polychromatique quelconque dont la couleur est représentée par la combinaison linéaire :

où désigne une source primaire monochromatique de longueur d'onde . Chacune des sources monochromatiques peut être décomposée sur les sources primaires , et selon l'égalité (1) ce qui conduit à :

où , et désignent les composantes trichromatiques spectrales déterminées une fois par toutes par la CIE à partir d'un panel d'observateurs (cf. ci-dessous). À partir des égalités (3) et (4) on obtient :

et par identification avec (1), on déduit les composantes , et :

On voit ainsi qu'une fois définies les composantes trichromatiques spectrales , et , tout stimulus coloré présentant un spectre peut être représenté par un point de coordonnées , et .

L'estimation des fonctions , et a été faite en 1926 par J. Guild [] avec 7 observateurs sur un champ visuel limité à un angle de 2° pour que les flux lumineux soient essentiellement incidents sur la macula (Cf. paragraphe Mécanisme de base de la vision des couleurs). Les primaires étaient choisies à 700nm pour le rouge ( ), 546,1nm pour le vert ( ) et 435,8nm pour le bleu ( ). Le champ d'observation est divisé en 2 parties (cf. figure 11), l'une est éclairée par une source monochromatique, l'autre reçoit les flux émis par les trois sources primaires qui se superposent pour donner lieu à une synthèse additive des couleurs. L'observateur ajuste l'éclairement du aux sources primaires en modifiant la position longitudinale des sources ou en occultant plus ou moins les flux émis à l'aide de diaphragmes calibrés. Le but est de parvenir à l'équivalence de perception visuelle des deux moitiés du champ d'observation.

Les composantes trichromatiques ainsi évaluées sont appelées les fonctions colorimétriques CIE , et . Elles sont tabulées depuis 1931 d'où le nom de système RGB CIE 1931. L'évolution des fonctions colorimétriques en fonction de la longueur d'onde est présentée en figure 12.

L'échelle des ordonnées est définie de telle façon que .

Ce choix se justifie par le fait que la perception visuelle d'un stimulus neutre (couleur blanche) correspond à une réponse équilibrée des trois types de cônes bleu, vert et rouge. Il faut également remarquer que pour des longueurs d'onde inférieures à 550nm, les courbes et présentent des ordonnées négatives. Ceci est du au fait qu'il est impossible de reproduire tous les rayonnements monochromatiques par synthèse additive des couleurs et qu'en conséquence, dans le dispositif décrit en figure 11, l'équivalence de perception visuelle des deux parties du champ d'observation n'est obtenue à certaines longueurs d'onde qu'en ajoutant au rayonnement monochromatique du flux issu des sources primaires.

D'après les égalités (5), un rayonnement polychromatique quelconque de luminance est associé à une couleur où les composantes trichromatiques dans le système RGB sont données par :

La chromaticité de la lumière ne dépendant que des valeurs relatives de ces composantes, on définit les coordonnées trichromatiques , et par :

Dans la pratique, il est plus aisé de représenter les couleurs dans un plan plutôt que dans l'espace. On utilise alors la relation déduite de (7) à savoir :

qui est l'équation d'un plan passant par les extrémités des vecteurs unitaires , et (cf. figure 13).

Une couleur est alors représentée par un point ( ) dans le plan. La coordonnée se déduisant simplement de la relation (8) si et sont connues, on adopte une représentation du plan 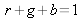sous la forme d'un triangle isocèle rectangle dans lequel et sont des axes de coordonnées rectangulaires (cf. figure 14). La représentation ainsi obtenue est appelée diagramme de chromaticité (rg). Il y est tracé le lieu des radiations monochromatiques (spectrum locus ou lieu spectral) pour correspondant aux coordonnées suivantes (avec ) :

ainsi que les couleurs primaires rouge ( ; =700nm), vert ( 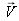; =546,1nm) et bleu ( ; =435,8nm). La droite joignant les extrémités rouge et bleu du spectre visible est appelée droite des pourpres.

Toutes les couleurs existantes ont leurs points associés à l'intérieur du domaine délimité par le lieu spectral et la droite des pourpres. Les points à l'extérieur de ce domaine n'ont pas de sens physique, ils correspondent à des stimuli irréels.

Comme on peut le constater sur la figure 14, certaines couleurs ont des coordonnées trichromatiques négatives dans le système RGB. Pour s'affranchir de cet inconvénient, il a été choisi d'opérer une transformation linéaire de l'espace RGB qui conduise à des fonctions colorimétriques , et n'ayant pas de valeurs négatives. Par ailleurs, les primaires , et ont été choisies afin que le plan soit le plan de luminance nulle et que l'axe soit l'axe des luminances visuelles. Comme pour un stimulus quelconque de luminance énergétique , la luminance visuelle correspondante est telle que :

avec en vision photopique et où est la fonction d'efficacité lumineuse relative spectrale (cf. cours de photométrie). Alors, en notation trichromatique d'où est identique à .

La transformation linéaire est définie par [] :

ce qui donne la dépendance en longueur d'onde indiquée en figure 15.

Une couleur quelconque est représentée par un vecteur de composantes trichromatiques , , 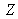telles que :

dont on tire les coordonnées trichromatiques , , telles que :

et comme , on représente les couleurs dans un repère plan à axes orthogonaux. Les couleurs monochromatiques pour ayant des coordonnées (avec ) données par :

elles se situent sur la courbe du lieu spectral (spectrum locus). Le domaine chromatique à l'intérieur duquel se situent toutes les couleurs réelles est limité par le lieu spectral et la droite des pourpres. L'ensemble est intégralement contenu dans le triangle , , représentant les primaires dont les coordonnées sont :

• pour la primaire :

• pour la primaire :

• pour la primaire :

Ces primaires sont irréelles puisqu'à l'extérieur du domaine chromatique (cf. figure 16).

La figure 17 montre le diagramme de chromaticité CIE 1931 avec les couleurs du domaine chromatique ainsi que le nom des zones de couleur pour un observateur adapté à la lumière du jour []. La zone centrale autour de la position du stimulus équiénergétique correspond aux illuminants normalisés de la CIE.

Par définition, la répartition spectrale du stimulus blanc équiénergétique est uniforme. On a donc d'où

et

puisque

Il en est de même dans l'espace 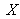, , pour lequel on a donc . Le point représentatif du stimulus 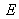se situe au centre du triangle RGB ou XYZ (cf. figures 14 et 16).

Dans le diagramme si une couleur résulte de la synthèse additive de deux couleurs et , la relation d'addition 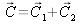se traduit par le fait que les points , et sont alignés selon une même droite (cf. figure 18).

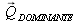De façon analogue une couleur quelconque peut s'exprimer comme l'addition du blanc équinergétique et d'une couleur pure (située sur le lieu spectral). Cette dernière sera appelée couleur dominante et .

Inversement le blanc équiénergétique peut en théorie être obtenu par addition d'une couleur et d'une couleur pure appelée couleur complémentaire tel que .

La quantité correspond à la pureté de la couleur . Le rapport vaut 0 pour le blanc équiénergétique et 1 pour une couleur monochromatique.