Métrologie optique par la transformation de Fourier fractionnaire

Résolution de l'équation de propagation par TF classique

Pour commencer, nous allons considérer le cas où une onde d'amplitude 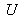se propage entre deux plans séparés d'une distance comme l'illustre la figure (3).

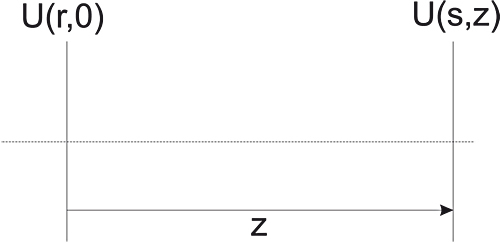
Figure 3 : Propagation d'une onde entre deux plans séparés d'une distance z
Figure 3 : Propagation d'une onde entre deux plans séparés d'une distance z [zoom...]Info

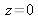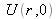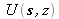Le plan de gauche est le plan d'origine situé en . Il contient l'amplitude du champ notée  avec  . Le plan de droite est le plan d'arrivée situé à une distance du plan d'origine. Il contient l'amplitude du champ notée avec  .

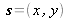La propagation entre deux plans en espace libre d'une onde est régie par l'équation différentielle suivante  :

(2.1)

où 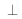 définit le champ transversal de 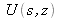 .  est le nombre d'onde et  la longueur d'onde.

Pour résoudre cette équation différentielle, nous pouvons utiliser la transformation de Fourier classique. En sachant que la transformation est définie par :

(2.2)

avec 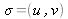 et de norme 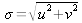 .  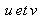sont les fréquences spatiales suivant les deux axes du système de coordonnées,  . Le produit scalaire nous donne 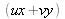 . L'équation différentielle (2.1) dans le domaine spectral devient alors :

(2.3)

Dans le domaine spectral, l'équation différentielle d'ordre deux sur les variables spatiales 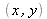et un sur la variable 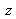se transforme en une équation d'ordre un sur la variable de propagation 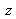. La solution de cette équation est :

(2.4)

L'expression de 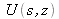dans le domaine spatial se détermine au moyen d'une transformation inverse de 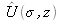, c'est-à-dire :

(2.5)

En insérant l'équation (2.4) dans (2.5), on obtient :

(2.6)

Nous sommes donc ici dans le cas d'une transformation de Fourier sur le produit de deux fonctions en  .

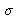Dans le domaine spatial, cela se traduit par un produit de convolution. En sachant que

(2.7)
(2.7) [zoom...]

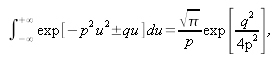
on obtient la valeur du champ après propagation tel que :

(2.8)
(2.8) [zoom...]

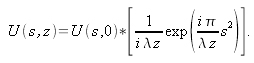
Le symbole * représente la convolution bidimensionnelle sur les variables spatiales. La forme intégrale de la relation (2.8) bien connue est :

(2.9)
(2.9) [zoom...]

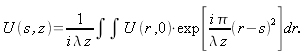
Nous retrouvons souvent cette expression sous sa forme développée telle que :

(2.10)
(2.10) [zoom...]

Dans ce paragraphe la TF classique a été utilisée pour résoudre l'équation de propagation.

La structure mathématique de l'intégrale de Fresnel est très proche de la structure de la TF fractionnaire. Il n'y a donc pas de raison pour que l'intégrale de propagation ne s'exprime pas au moyen de la transformation de Fourier fractionnaire.

Le paragraphe qui suit expose la méthode.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Propagation en espace libre et TF fractionnaireDescription de la propagation par TF fractionnaire