
Description de la propagation par TF fractionnaire
Dimensionnement des variables
La définition mathématique de la transformation de Fourier fractionnaire est la suivante :
avec
où
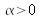 .
.
Comme nous pouvons le constater, si l'on souhaite décrire la propagation au moyen de variables spatiales, la définition de la TF fractionnaire pose problèmes puisque ses variables sont sans dimensions. Ceci constitue la première problématique. Une solution a été proposé par . Cette solution consiste à donner une interprétation optique de la TF fractionnaire dans l'espace de Wigner.
Reste ensuite à trouver les éléments optiques de cette interprétation.
La TF fractionnaire d'ordre
 d'une fonction fait subir une rotation d'angle
d'une fonction fait subir une rotation d'angle
 dans le sens horaire à sa distribution de Wigner.
dans le sens horaire à sa distribution de Wigner.
Lohmann a décomposé cette rotation en trois étapes comme l'illustre la figure (4).
Figure 4 : (a) Contour d'origine, (b) Etirement fréquentiel, (c) Etirement spatial, (d) Etirement fréquentiel. x, variable spatial,
 variable fréquentiel
variable fréquentiel
Cette illustration est pour un angle
 de
de
 .
.
Ces trois étapes se résument à un étirement fréquentiel de la distribution, suivi d'un étirement spatial et enfin un dernier étirement fréquentiel. Les étirement fréquentiels sont réalisés optiquement par une lentille et l'étirement spatial par un produit de convolution, autrement dit une propagation. Dans , le paramètre
 apparaît sous la forme d'une focale abstraite
apparaît sous la forme d'une focale abstraite
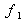 dépourvue de sens physique. Cette ambiguité a été soulevée en remplaçant le paramètre
dépourvue de sens physique. Cette ambiguité a été soulevée en remplaçant le paramètre
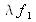 par
par
 dans l'interprétation de la TF fractionnaire par la distribution de Wigner.
dans l'interprétation de la TF fractionnaire par la distribution de Wigner.
Cette interprétation de la TF fractionnaire est telle que
où les variables
 ,
,
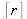 et
et
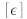 ont la dimension d'une longueur. Le coefficient de normalisation
ont la dimension d'une longueur. Le coefficient de normalisation
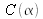 vaut quant à lui :
vaut quant à lui :
Pour
 et des variables sans dimensions, la définition mathématique de la transformation de Fourier fractionnaire est retrouvée. Dans notre cas, la définition donnée à
et des variables sans dimensions, la définition mathématique de la transformation de Fourier fractionnaire est retrouvée. Dans notre cas, la définition donnée à
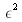 est liée à la façon dont on échantillonne le signal et à l'expression de la TF numérique. Car c'est bien le numérique qui nous sert pour une métrologie par TF fractionnaire. Pour définir la valeur de
est liée à la façon dont on échantillonne le signal et à l'expression de la TF numérique. Car c'est bien le numérique qui nous sert pour une métrologie par TF fractionnaire. Pour définir la valeur de
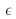 , il est nécessaire d'écrire la définition de la TF fractionnaire dans le cas particulier où
, il est nécessaire d'écrire la définition de la TF fractionnaire dans le cas particulier où
 :
:
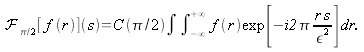
Sa version discrétisée vaut :
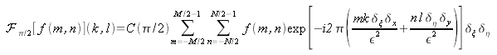
où
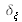 et
et
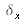 représentent le pas d'échantillonnage de
représentent le pas d'échantillonnage de
 et de sa transformée suivant les abscisses et
et de sa transformée suivant les abscisses et
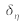 et
et
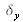 suivant les ordonnées.
suivant les ordonnées.
Le nombre d'échantillons suivant l'axe des abscisses est M et N suivant les ordonnées.
Que nous soyons dans le domaine spatial ou le domaine spectral, le nombre d'échantillons est le même.
La relation (2.16) doit s'écrire comme la transformation de Fourier discrète proposée par des logiciels, c'est-à-dire :
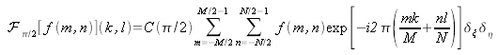
En identifiant les relations (2.17) et (2.16), nous obtenons :
La TF numérique ne "voit" que des pixels, sans dimension, au même titre que la FFT (Fast Fourier Transform).
Donc quelques soient les domaines de description (spatial ou fréquentiel), c'est le pixel qui échantillonne.
C'est la raison pour laquelle nous posons :
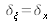 et
et
 .
.
Généralement les pixels sont identiques suivant les deux axes du plan de description et pour tous domaines de description donc le pas d'échantillonnage est pris égale à
 .
.
Le nombre de pixels suivant les deux axes est généralement le même :
 . Si ce n'est pas le cas, on tronque les dimensions de l'image pour obtenir une image carrée. Finalement, nous avons :
. Si ce n'est pas le cas, on tronque les dimensions de l'image pour obtenir une image carrée. Finalement, nous avons :
Si l'image ne peut pas être de dimensions carrées, on définie deux
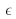 comme
comme
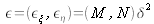 .
.
Courbures résidus
La transformation de Fourier est un cas particulier de la TF fractionnaire, nous pouvons alors écrire que :
A partir de cette définition de la TF, l'équation (2.4) devient :
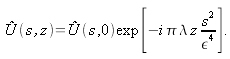
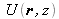 est la transformée de Fourier inverse de
est la transformée de Fourier inverse de
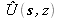 :
:

que l'on peut également énoncer comme étant une transformation de Fourier fractionnaire d'ordre
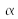 telle que :
telle que :
où
et d'ordre fractionnaire :
Puisque la distribution du champ
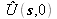 est la transformée de Fourier fractionnaire d'ordre
est la transformée de Fourier fractionnaire d'ordre
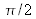 de
de
 , alors par composition
, alors par composition
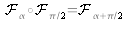 , nous pouvons définir la distribution d'amplitude du champ à une distance
, nous pouvons définir la distribution d'amplitude du champ à une distance
 en fonction de la distribution d'amplitude à la distance
en fonction de la distribution d'amplitude à la distance
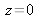 en faisant apparaître une transformation de Fourier fractionnaire d'ordre
en faisant apparaître une transformation de Fourier fractionnaire d'ordre
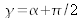 en facteur avec un terme de phase quadratique telle que :
en facteur avec un terme de phase quadratique telle que :
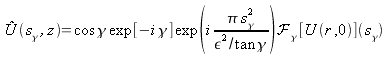
La relation (2.26), d'après Bonnet et Pellat-Finet
, met en évidence le problème du résidu de phase quadratique dépendant de la variable
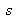 . Lorsque l'on considère la diffraction dans l'approximation de Fraunhofer, une transformation de Fourier pure est suffisante. Dans cette approximation les termes de phase quadratique n'interviennent pas. Autrement dit, les courbures n'interviennent pas. Seuls sont considérés les plans.
. Lorsque l'on considère la diffraction dans l'approximation de Fraunhofer, une transformation de Fourier pure est suffisante. Dans cette approximation les termes de phase quadratique n'interviennent pas. Autrement dit, les courbures n'interviennent pas. Seuls sont considérés les plans.
Dans le cas de l'approximation de Fresnel, nous avons vu que la transformation de Fourier fractionnaire peut être utilisée mais cette interprétation laisse un terme de phase quadratique. Il ne s'agit donc pas d'une TF fractionnaire pure. La notion de plan n'est donc pas adaptée à l'analyse des systèmes d'imagerie en éclairage cohérent.
La théorie métaxiale apparaît comme un prolongement de la théorie de l'optique paraxiale.
Bonnet explique clairement la démarche :
la recherche d'une imagerie cohérente impose que l'équation (2.26) ne contienne pas le terme
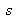 qui l'affecte. Ce terme de phase quadratique fait allusion à la notion de transparence de courbure. Cette transparence de courbure devient neutre pour une courbure particulière
. Nous trouvons donc une image cohérente sur un récepteur sphérique.
qui l'affecte. Ce terme de phase quadratique fait allusion à la notion de transparence de courbure. Cette transparence de courbure devient neutre pour une courbure particulière
. Nous trouvons donc une image cohérente sur un récepteur sphérique.
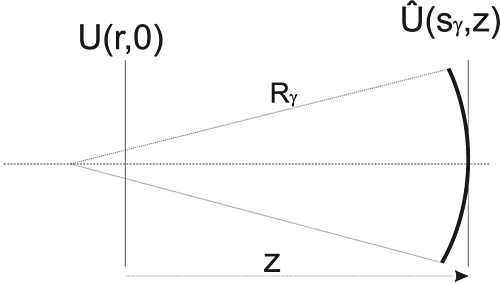
Figure 5 : Image cohérente sur la calotte sphérique de courbure
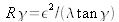
L'image cohérente de
 se trouve donc sur une sphère de rayon de courbure
se trouve donc sur une sphère de rayon de courbure
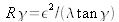 comme l'illustre la figure (5).
comme l'illustre la figure (5).
La définition du champ sur la calotte sphérique est définie par :
avec les changements d'échelle suivants :
Cette transformation d'ordre fractionnaire
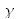 implique une modification de la relation (2.25) :
implique une modification de la relation (2.25) :
Les propriétés de la TF fractionnaire deviennent intéressantes dans le cas de la description de la propagation.
Si
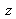 tend vers 0, l'ordre
tend vers 0, l'ordre
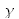 est nul. L'opérateur fractionnaire tend alors vers
est nul. L'opérateur fractionnaire tend alors vers
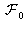 qui est l'opérateur identité.
qui est l'opérateur identité.
Si maintenant
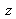 tends vers l'infini,
tends vers l'infini,
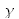 tend vers
tend vers
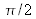 . Il s'agit de l'opérateur TF classique.
. Il s'agit de l'opérateur TF classique.
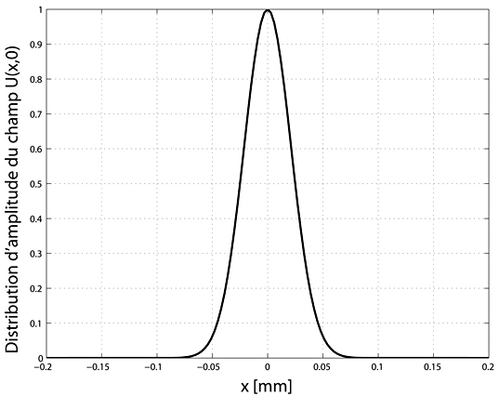
Figure 6 : (a) fonction gaussienne à
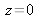 avec
avec
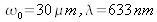
Du point de vue de la diffraction, il s'agit de la diffraction dans l'approximation de Fraunhofer.
Nous passons donc continûment du champ initial à son spectre angulaire.
la notion théorique de récepteur sphérique ne présente pas d'inconvénient particulier dans la plupart de nos méthodes de métrologie. Le récepteur est un capteur quadratique sensible uniquement à l'intensité. Le terme de phase en
 de l'équation (2.26) n'intervient donc pas.
de l'équation (2.26) n'intervient donc pas.
Exemple
Prenons un faisceau gaussien tel que son amplitude est définie par :
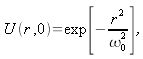
avec
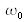 le rayon du faisceau à
le rayon du faisceau à
 . La figure (6) donne une représentation graphique.
. La figure (6) donne une représentation graphique.
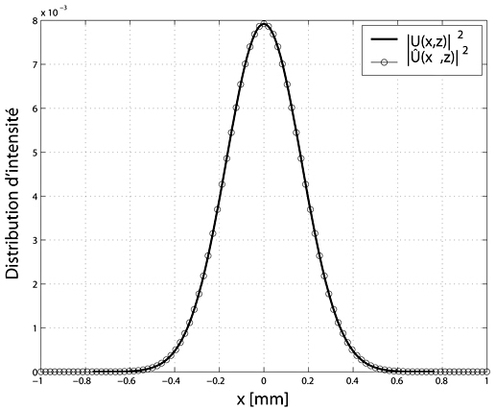
Figure 7 : Distributions d'intensité à
 avec
avec
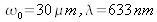
La distribution d'amplitude du faisceau gaussien à une distance
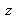 compte tenu de la relation de Fresnel (2.10) vaut :
compte tenu de la relation de Fresnel (2.10) vaut :
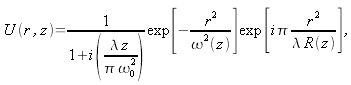
avec
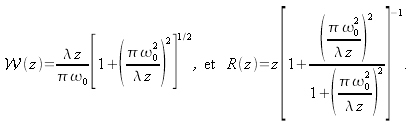
La comparaison des distributions d'intensité
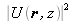 et
et
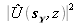 pour
pour
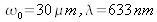 et
et
 est illustrée figure (7).
est illustrée figure (7).
L'ordre fractionnaire
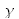 vaut, quant à lui,
vaut, quant à lui,
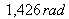 et la distribution d'amplitude
et la distribution d'amplitude
 se trouve sur une sphère de rayon de courbure
se trouve sur une sphère de rayon de courbure
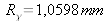 .
.