Approximations de Born

L'utilisation des approximations de Born en diffusion est courante et justifiée lorsque le rayonnement interagit peu avec la matière [ ]. Elles sont particulièrement appréciées quand elles permettent de simplifier le formalisme au point de rendre l'écriture d'expressions analytiques envisageable pour R et T. Principalement elles reviennent à négliger:

• les réflexions multiples

• la réfraction dans les matériaux

• les variations de phase dues aux modifications de la vitesse de propagation au passage d'un milieu à l'autre.

La seconde et la troisième de ces simplifications peuvent être appelées "approximations cinématiques", puisque la conservation n'est plus vérifiée que pour le vecteur de vitesse le long de la trajectoire de la particule. Au contraire, les modèles précédents ("dynamiques") respectent les lois de la conservation mécanique.

Pour les films multicouche, l'intégrale de l'expression précédente devient une somme discrète. Quand l'origine des cotes (z=0) est prise à la surface libre du film, on obtient :

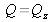En appliquant les approximations de Born, nous avons retracé les réflectivités de l'échantillon présenté précédemment suivant la théorie dynamique. On voit sur la figure que ces approximations ne sont pas valides dans la région qui s'étend des très petits angles jusqu'à plusieurs fois l'angle critique du film (soit des petits vecteurs de diffusion avec dans les conditions spéculaires). Cette limitation rend l'utilisation des approximations de Born délicates quand l'intensité réfléchie chute rapidement avec .