Quelques fonctions fréquemment utilisées et leur Transformée de Fourier
Définition
![[zoom...]](javascript:window.open(%22../res/Tablo01_1.png%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
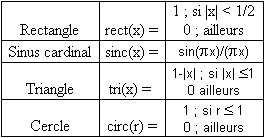
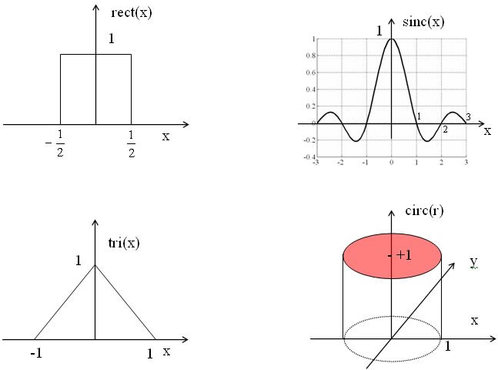
Représentation graphique
![[zoom...]](javascript:window.open(%22../res/image_I_01_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
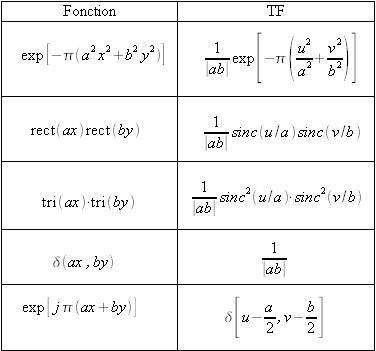
Couples de transformées relatifs à quelques fonctions séparables en coordonnées cartésiennes
![[zoom...]](javascript:window.open(%22../res/Tablo02_1.png%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
La fonction cercle et sa Transformée de Fourier
La relation (I-2) pour les fonctions à symétrie circulaire (au paragraphe 'fonctions à symétrie circulaire') s'applique ici avec :
En remplaçant (I-3) dans (I-2) il vient :
Posons
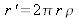, les bornes de l'intégrale dans la relation (I-4) deviennent 0 et
.
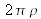donc
Compte tenu de l'identité :
où J1(x) est définie comme la fonction de Bessel d'ordre 1, on trouve finalement que :
L'allure de cette fonction est donnée dans la figure I-2 qui suit.
![[zoom...]](javascript:window.open(%22../res/image_I_02_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
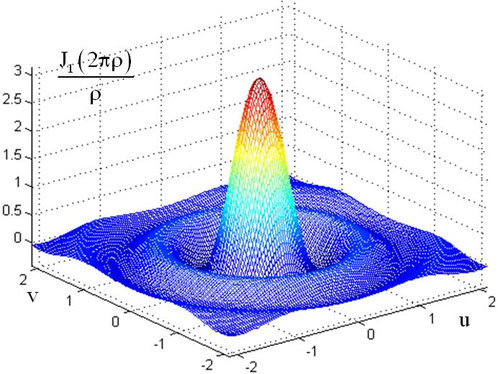
Notons que la TF de la fonction cercle est à symétrie circulaire. Elle se compose d'un pic central et d'une série d'anneaux concentriques d'amplitudes décroissantes.
![[zoom...]](javascript:window.open(%22../res/image_I_03_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
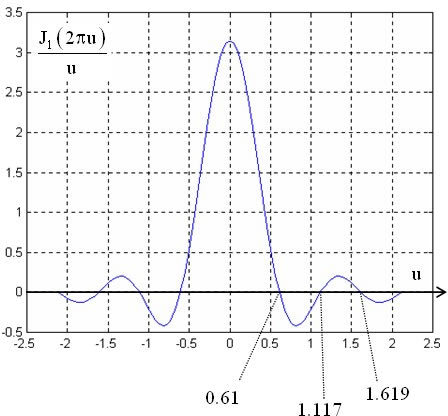
La figure I-3 représente un profil radial de cette fonction. Les zéros ne sont pas également espacés le long d'un rayon comme c'est le cas pour la fonction sinus cardinal. On peut noter aussi que le rayon du lobe central est égal à 0,61.