
Cas de l'éclairage incohérent
Introduction
Dans le cas de l'éclairage (spatialement) cohérent (voir figure V-3) tous les points de l'objet ont une amplitude complexe dont la phase varie dans le temps de la même façon.
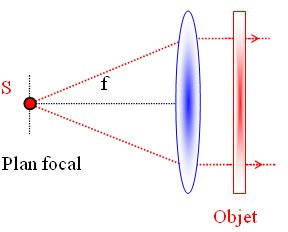
Expérimentalement ceci est réalisé en plaçant une source suffisamment petite dans le plan focal objet d'une lentille.
L'éclairage est dit (spatialement) incohérent si la source est relativement large (voir figure V-4).
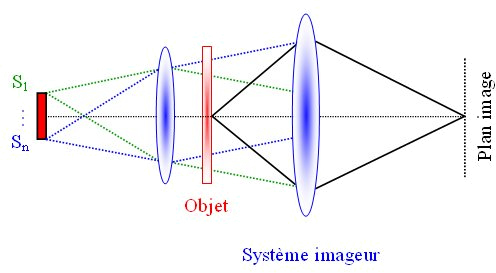
Les amplitudes complexes des différents points composants la source varient de façon aléatoire. Entre un train d'onde issu de S1 et un autre issu de Sn la relation de phase disparaît et la moyenne temporelle sur le terme d'interférence sera nulle.
Ce sont donc les intensités que l'on doit sommer.
On écrit l'image dans ce cas comme une transformation linéaire de l'intensité [] :
L'intensité dans l'image est une convolution de l'intensité idéale (obtenue par l'optique géométrique) et d'une réponse impulsionnelle proportionnelle au carré du module de la réponse impulsionnelle obtenue avec un éclairage cohérent.
Réponse fréquentielle d'un système optique (éclairage incohérent)
Définissons les spectres normalisés de Ig et Ii :
Les spectres sont normalisés par rapport à la valeur de l'intégrale aux fréquences nulles qui représente la composante continue ou le fond continu de l'image.
D'une façon analogue on définit la fonction de transfert normalisée du système :
En appliquant le théorème de convolution à l'Eq. V-2, il vient :
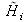 est appelée la «fonction de transfert optique» ou encore la «fonction de transfert de modulation» («FTM»).
est appelée la «fonction de transfert optique» ou encore la «fonction de transfert de modulation» («FTM»).
Relation entre la FTM et la fonction de transfert cohérente
En appliquant le théorème d'autocorrélation :
En faisant le changement de variable u''=u'-u/2 et v''=v'-v/2 , on peut rendre l'expression précédente symétrique :
Or pour le système cohérent nous avons
 , donc
, donc
Où on a remplacé u'' par u' et remplacé P² par P au dénominateur car P=1 ou 0. La relation (V-3) servira de lien fondamental entre les systèmes cohérents et incohérents.
L'expression de
 fait apparaître l'aire de la partie commune à deux fonctions pupillaires identiques :
fait apparaître l'aire de la partie commune à deux fonctions pupillaires identiques :
-
l'une centrée au point de coordonnées :
 ,
,
-
l'autre au point diamétralement opposé de coordonnées
 .
.
Le dénominateur normalise cette aire par l'aire totale de la pupille (voir figure V-5).

Pour plus de détails concernant ce sujet, le lecteur pourra consulter la référence [ ] et les références à l'intérieur.
Résumé
Le système en éclairage cohérent est linéaire en amplitude. L'intensité est donnée par
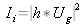 .
.
Le système en éclairage incohérent est linéaire en intensité. L'intensité est donnée par
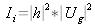 .
.
Le spectre fréquentiel de l'intensité image s'écrit :
-
en cohérent :
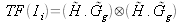 .
.
-
en incohérent :
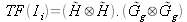 .
.
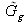 est le spectre de Ug,
est le spectre de Ug,
 est la fonction de transfert cohérente.
est la fonction de transfert cohérente.
* désigne la convolution : .
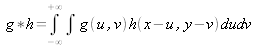
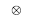 désigne l'auto-corrélation :
désigne l'auto-corrélation :
 .
.