Lois de la réfraction
Considérons une surface S de l'espace, séparant deux milieux d'indices respectifs n1 et n2 contenant respectivement les point A et B. Le trajet effectivement suivi par la lumière pour aller de A à B passe par le point I sur la surface.
AI est le rayon incident, IB est le rayon réfracté.
L = n1.AI + n2.IB est le chemin optique (AIB).
Un petit déplacement dI de I provoque une variation dL telle que dL/dI = 0 en vertu du principe de Fermat. L'expression (3) appliquée aux parcours AI et IB donne :
de même
Puisque
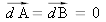 , finalement :
, finalement :
Si
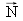 est le vecteur unitaire dans la direction de la normale,
est le vecteur unitaire dans la direction de la normale,
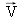 celui dans la direction
celui dans la direction
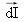 .
.
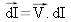 soit :
soit :
Le principe de Fermat imposant, pour un trajet effectivement suivi par la lumière, dL/dI = 0 pour tout
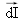 ,
,
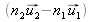 et
et
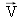 sont perpendiculaires donc
sont perpendiculaires donc
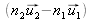 et
et
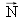 sont parallèles.
sont parallèles.
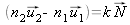 montre que
montre que
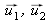 et
et
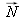 appartiennent à un même plan P.
appartiennent à un même plan P.
P est le plan d'incidence, il contient le rayon incident, le rayon réfracté et la normale à la surface en I, i1 et i2 sont, dans ce plan, les angles entre les rayons incidents et réfractés par rapport à la normale. On en déduit la relation de réfraction vectorielle :
Et, par projection dans le plan de la surface :
Les lois de Descartes se déduisent des relations précédentes:
Loi 1 : Le rayon réfracté est dans le plan d'incidence
Loi 3 : Les angles i1 et i2 des rayons incidents et réfléchis sont tels que n1.sini1 = n2.sini2
La loi 2 concerne les surfaces réfléchissantes, pour lesquelles i1 = - i2 . On verra par la suite que les formules des surfaces réfractantes s'appliquent aux surfaces réfléchissantes en prenant : n2=-n1.
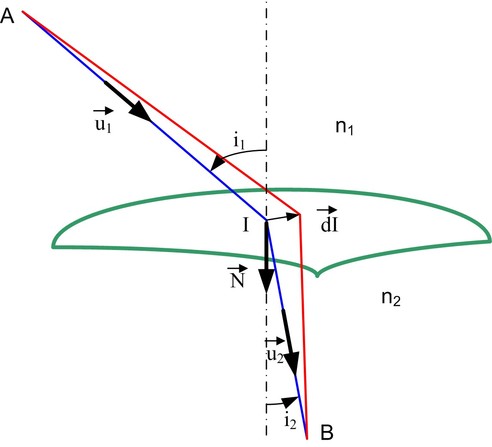
Réfraction
Considérons deux milieux d'indices n1 et n2, la troisième loi de Descartes nous donne la relation entre les angles d'incidence et de réfraction dans les deux milieux :
Cette relation est parfaitement symétrique, en accord avec le principe du retour inverse de la lumière. Un rayon venant du deuxième milieu faisant l'angle i2 avec la normale fera, après réfraction par la surface, un angle i1 dans le premier milieu satisfaisant à la relation (5).
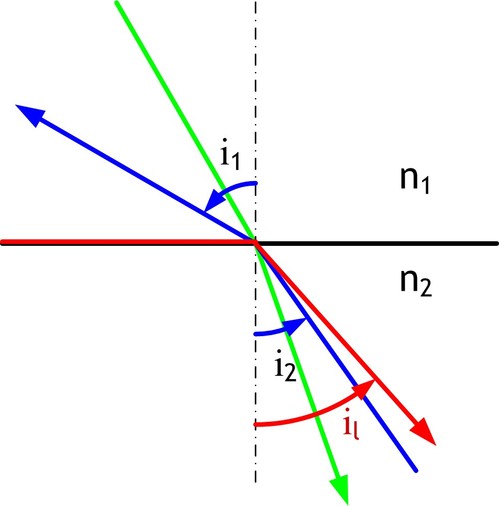
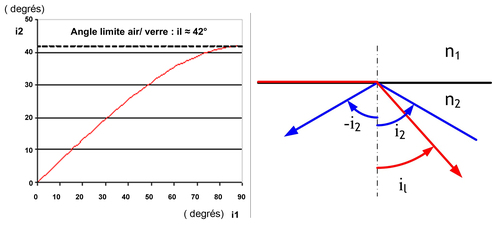
Angle limite
Pour il = 90°, incidence rasante, le rayon réfracté fait, avec la normale l'angle i2 tel que : sini2=n1/n2.
i2 est alors appelé l'angle limite il
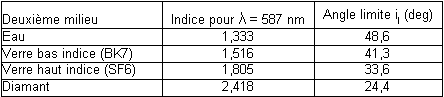
Tout rayon provenant du deuxième milieu dont l'angle d'incidence i2 est supérieur à il subit une réflexion totale. Si le premier milieu est l'air (n1=1), le tableau ci-dessous donne quelques valeurs de il :
Réflexion totale dans une fibre optique multimodale :
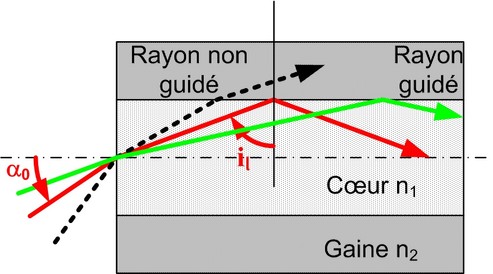
L'indice du cœur est n1, l'indice de la gaine est n2< n1.
Un rayon lumineux qui a une incidence supérieure à i1 sur l'interface cœur-gaine se réfléchit totalement, il est guidé.
Son incidence à l'entrée de la fibre est inférieure à
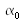 .
.
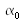 est le demi-angle d'ouverture de la fibre. L'ouverture numérique de la fibre est :
est le demi-angle d'ouverture de la fibre. L'ouverture numérique de la fibre est :