Description du filtrage
Dans le cas du contraste de phase, le filtrage dans le plan de Fourier consiste à déphaser de
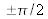radians et à atténuer le point lumineux central. Voir Fig.13a. Ceci peut être réalisé en pratique en plaçant dans le plan de Fourier une lame de verre à faces planes et parallèles de grande qualité sur une face de laquelle on a déposé en son centre un minuscule disque d'une épaisseur appropriée d'un matériau diélectrique absorbant (souvent de l'aluminium). Voir Fig.13b. Cette lame est appelée ‘lame de phase'. On la positionne de manière à ce que le disque recouvre le point lumineux.
![[zoom...]](javascript:window.open(%22../res/C_fig13_2.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
En négligeant la taille finie du disque, le montage par double diffraction donne alors, si
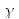représente le coefficient d'atténuation (en amplitude) du point lumineux central (
) :
Le facteur
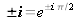devant le terme
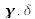traduit le déphasage de
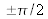introduit par la lame de phase.
L'éclairement, proportionnel au module carré de l'amplitude complexe, a donc pour expression
en négligeant le terme non significatif du deuxième ordre
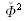devant les autres termes dans ce calcul au premier ordre.
Les variations de phase de l'objet sont alors perçues comme des variations de luminosité sur un fond plus ou moins clair. (Cf. Figure 7f).
Les variations d'éclairement de l'image sont proportionnelles aux variations de phase de l'objet.
Suivant que le point lumineux central dans le plan de Fourier verra sa phase retardée ou respectivement avancée (i.e. déphasage de respectivement
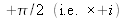et
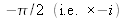en convention
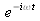), un retard de phase dans le front d'onde (chemin optique parcouru dans l'objet plus grand;
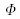positif en convention
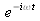) sera perçu comme plus ou respectivement moins lumineux que le fond, et vice versa pour une avance de phase. On parle dans le premier cas (détail plus lumineux pour un retard de phase) de contraste de phase négatif et dans le second de contraste de phase positif (cf. []). Les anglo-saxons parlent eux respectivement de contraste de phase “brillant” (bright phase contrast) ou “sombre” (dark phase. constrast.) en se référant à la manière dont apparaît un excès de chemin optique dans l'objet (cf. []).
On peut noter que sans atténuation, c'est à dire pour
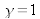, l'éclairement observé par l'œil ou une caméra serait proportionnel à
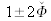et serait donc de très faible contraste puisque
.
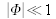Le contraste C de l'image obtenue, rapport des variations caractéristiques de luminosité sur la valeur moyenne de cette dernière, s'exprime donc par :
où
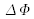représente les variations typiques de phase au sein de l'objet.
Le contraste est d'autant meilleur que
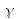est petit, c'est à dire que l'atténuation est importante. (Pour
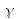strictement nul, les résultats précédents ne sont pas applicables ; on retombe en fait sur le cas de la strioscopie traité au paragraphe précédent).
En pratique, la taille finie du disque atténuant et déphasant altère (atténue) en fait également
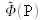pour les points P très proches du centre, qui correspondent aux très basses fréquences spatiales. La méthode du contraste de phase n'est donc pas adaptée pour mettre en évidence des variations spatiales de phase lentes dont la longueur typique de variation est, par exemple, de l'ordre de la moitié ou du quart du champ observé. Il est également à noter que la taille finie de la pupille de sortie de l'objectif du microscope, non décrite dans le formalisme simple précédemment décrit, implique également une coupure haute brutale de la fonction de transfert des fréquences spatiales qui induit un phénomène de Gibbs donnant des oscillations artificielles (franges) aux voisinages des variations rapides de phase de l'objet.
D'un point de vue expérimental, il est difficile de réaliser un déphasage précis de
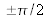, a fortiori simultanément pour toutes les longueurs d'onde du visible dans le cas d'un éclairage standard en lumière blanche. En fait, la transformation des variations de phase en variation d'éclairement fonctionne toujours, mais un peu moins efficacement, si on s'éloigne de la valeur idéale du déphasage. Par exemple, une erreur de
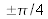par rapport à la valeur visée de
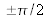ne produit qu'une chute de ~30% du contraste. De surcroît, si l'objet observé introduit simultanément des petites variations de phase et de transmission, cas relativement courant pour des objets biologiques, le déphasage optimal n'est plus d'exactement
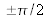mais dépend de l'objet (cf. [ et ]). Il s'avère en pratique que la valeur précise du déphasage introduit n'est pas cruciale pour des observations qualitatives des détails de l'image. A contrario, le montage du contraste de phase n'est jamais utilisé pour faire des mesures de déphasage, mais seulement pour mettre en évidence l'existence de variations spatiales de phase dans un objet bidimensionnel.