L'opérateur Laplacien
Les opérateurs de gradient vus précédemment exploitent le fait qu'un contour dans une image correspond au maximum du gradient dans la direction orthogonale au contour. Or le passage par zéro de la dérivée seconde d'une rupture d'intensité permet également de mettre en évidence le contour. La dérivée seconde est donc déterminée par le calcul du Laplacien :
qui peut s'écrire :
or on peut définir :
et :
Ainsi le Laplacien peut s'écrire :
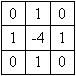
Cette opération de calcul de Laplacien peut alors être appliquée à une image par l'intermédiaire d'un filtrage avec le masque 3*3 suivant :
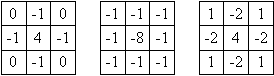
D'autres masques peuvent être utilisés
Après le filtrage de l'image au moyen d'un de ces filtres, il s'agit de détecter les passages par zéro en conservant uniquement les passages les plus marqués. En effet, la technique est particulièrement sensible au bruit en raison de la double dérivation. Il s'agit donc de ne pas considérer le bruit, qui peut très bien se traduire par des oscillations autour de zéro, comme un contour. C'est le rôle du seuil S qui va être utilisé dans cette approche pour ne prendre en compte que les passages par zéro d'amplitude relativement élevée correspondant à des vrais contours de l'image.
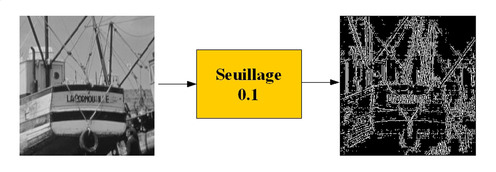
Une animation dans l'étude de cas permet de paramétrer le seuil après le calcul du Laplacien.