Le filtre de Marr ou Laplacien de Gaussienne ou chapeau mexicain

Le remède contre la sensibilité au bruit de la double dérivation est à la base des travaux de Marr qui ont débouché sur l'utilisation d'un filtre gaussien en guise de filtre passe-bas pour h(x,y). Le choix de ce filtre a été établi en raison du principe d'Heisenberg qui stipule que l'on ne peut pas améliorer en même temps la résolution spatiale ∆x et la résolution fréquentielle ∆f :

Dans le cas d'une détection d'un contour, celui-ci étant localisé spatialement et en fréquence, il est clair que les intervalles ∆x et ∆f doivent être petits. Détecter une rupture d'intensité implique une analyse des pixels voisins mais le voisinage ne doit pas être trop étendu. Filtrer l'image a pour conséquence de réduire les variations d'intensité, ce qui doit être raisonnable. Le filtre doit en effet avoir une largeur spectrale limitée. Or c'est la fonction gaussienne qui permet d'obtenir l'égalité dans le principe d'Heisenberg, d'où ce choix qui se traduit par :

La dérivée de la fonction gaussienne bi-dimensionnelle s'écrit alors :

Et la dérivée seconde s'exprime :

L'allure de h''(x,y), réponse impulsionnelle du filtre Laplacien de Gaussienne (LOG), lui a valu l'appellation « chapeau mexicain ». La mise en œuvre d'une détection de contours avec le filtre LOG nécessite les étapes suivantes :

• Convolution de l'image avec le filtre LOG (filtre 2D) ;

• Détection des passages par zéro de l'image résultante ;

• Seuillage de l'image afin de ne considérer que les passages par zéro d'amplitude suffisante.

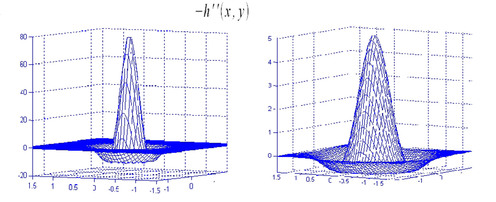
Le traitement repose sur cinq paramètres :

• N représente la taille du masque (matrice carrée) implantant le filtre LOG. N est impair.

• σ permet d'ajuster la taille du chapeau mexicain.

• ∆x et ∆y sont les pas d'échantillonnage utilisés pour discrétiser h''(x,y). Généralement ∆x = ∆ y

• S est le seuil qui permet de sélectionner les contours les plus marqués.

En fonction du pas d'échantillonnage, l'étendue spatiale vaut : .

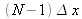Cette étendue peut aussi s'écrire en fonction de σ : avec k entier.

En prenant par exemple 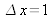, il s'agit de choisir N et σ de sorte que l'étendue du chapeau mexicain soit pertinente. Pour le chapeau mexicain, la valeur de k doit être au moins de 4.