Equations des hologrammes de fibre

Soit un objet opaque, noté 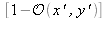 localisé à une distance 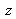 du capteur CCD, comme le montre la figure 8. En accord avec l'intégrale d'Huygens et sous l'approximation de Fresnel, l'amplitude du champ complexe, notée 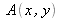est donnée par :

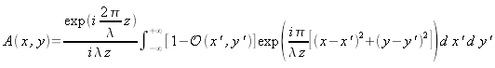
Dans le cas particulier où la transmittance de l'objet s'exprime par une fonction unidimensionnelle, l'équation (3.1) s'exprime sous une forme simplifiée :

Pour une fibre opaque de diamètre d et centrée à l'origine, la transmittance d'un tel objet est définie par la relation suivante :

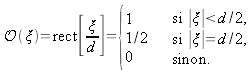
Le champ complexe s'exprime, à l'aide des intégrales de Fresnel de première et seconde espèce :

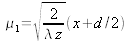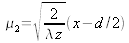où  et . et sont les intégrales de Fresnel de première et seconde espèce. Leur définition est :

Dans l'approximation champ lointain, c'est-à-dire lorsque , la distribution d'intensité s'exprime par la relation suivante :

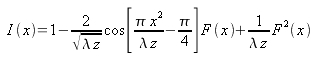
La figure 9 donne un exemple de distribution d'intensité. L'expression

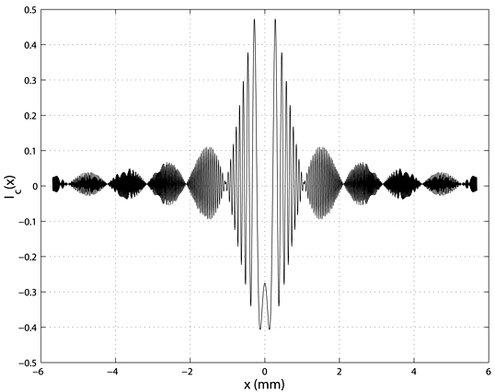
Figure 9 : Représentation de la distribution d'intensité 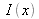pour et

est la transformée de Fourier de . Comme le montre l'équation (3.6), l'intensité I(x) est partiellement décrite par une fonction réelle à dérive de fréquence linéaire

Nous allons montrer qu'il est possible d'analyser ce type de signal par la TF fractionnaire. Dans la mesure où l'approximation champ lointain est moins restrictive que l'approximation champ proche, nous raisonnerons dans un premier temps sur l'équation (3.6). Les résultats resteront valables en champ proche.

Comme nous l'avons fait remarquer dans le cours ou dans le chapitre précédent, la propriété la plus importante de la transformation de Fourier fractionnaire est celle qui la relie à la fonction de distribution de Wigner. Nous allons donc tout d'abord étudier au paragraphe suivant la fonction de distribution de Wigner du second terme de l'équation (3.6).

Rappelons que la fonction de distribution de Wigner est définie par la forme intégrale :

Prenons le cas d'une fonction  définie par

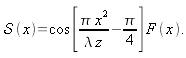
La fonction est la somme de deux termes exponentiels :

avec

La distribution de Wigner est bilinéaire. Elle fera donc apparaître un terme non-linéaire (on parle d'interférences) dans le cas d'un signal multi-composantes. La distribution de Wigner de la relation (3.10) vaut finalement :

Par la méthode des phases stationnaires, le développement du terme non linéaire, noté ici 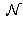 , donne le résultat qui suit :

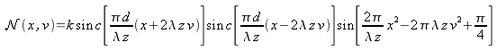
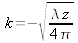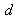avec  . Nous voyons clairement que les termes d'interférence contiennent toutes les informations liées au système, c'est-à-dire l'information sur la position axiale  et le diamètre  de la fibre.

Or une étude sur cette partie du signal ne paraît pas triviale pour la description des figures de diffraction.

Nous concentrerons donc notre attention sur les deux premiers termes de l'équation (3.13).

En sachant que 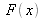 est la transformée de Fourier de et en vertu des relations (2.32), (2.33) et (2.34) du premier cours sur les fondements de la TF fractionnaire et ses propriétés envers la distribution de Wigner, les deux premiers termes de l'équation (3.13) peuvent être écrits comme la somme des distributions de Wigner suivantes :

où

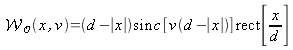
 est la fonction de distribution de la fonction rectangle définie par (3.3)

La figure 10 donne un exemple de distribution de Wigner de  .

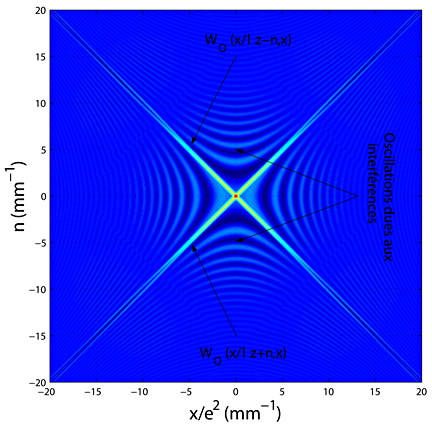
Figure 10 : Représentation de la distribution de Wigner de pour et le nombre d'échantillons et le pas d'échantillonnage

Pour cet exemple, la distance  choisie vaut 100mm et le diamètre d vaut 60 µm.

Ce graphe met en évidence les deux distributions 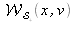 et 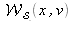 ainsi que les quatre zones d'interférences externes liées à la bilinéarité de l'opérateur.

Les deux branches de distribution sont concentrées autour des lois de variation  .

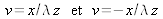La distribution de Wigner conserve l'ouverture de la fonction sur laquelle elle s'applique.

La largeur de chacune des branches correspond donc au diamètre d de l'ouverture de la fonction rectangle .

La distribution d'intensité 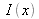 (équation (3.6)) a été tracée figure 9. Dans ce cas, la constante a été soustraite.

Cette opération permet de mettre clairement en évidence la distribution de Wigner du signal utile.

En effet, dans l'espace de Wigner, une constante se traduit par une impulsion de Dirac qui empêche toute description du signal.

A la représentation figure 9 est associée sa représentation dans l'espace de Wigner que l'on note 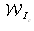 (figure 11).

Figure 11 : Représentation de la distribution de Wigner de 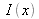, notée 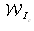pour et

Nous pouvons constater les effets du terme d'auto-corrélation de la fonction 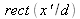 sur les termes d'interférence.

Compte tenu de la relation qui lie la fonction de distribution de Wigner et la transformation de Fourier fractionnaire, nous allons mettre à contribution cette transformation pour restituer les hologrammes de fibre.