Why using two cameras?

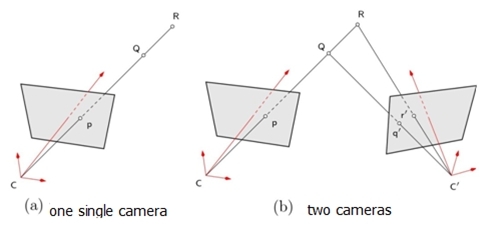
If we reason from a geometric point of view, a camera is a sensor which transforms every “visible point” of the tridimensional space into a point of the image's bidimensional space. Therefore, this transformation suppresses the third dimension and is, thus, irreversible. It is graphically expressed by Figure 11.a: both points 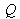and 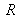of the space project themselves on the image plane in a single and only point 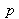because they are on the same projection line 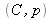, 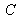is called the projection center or optical center. It means that given an image point 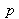, there is an infinity of tridimensional points that can be the projection of it. By using two cameras, as shown on figure 11.b, it is possible to determine the point tridimensional position by triangulation. Indeed, there is only one point of space corresponding to the pair of projected points 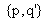and only one corresponding to 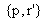. Therefore, the triangulation consists in determining the intersection in the space of two projection lines. Thus, it is necessary to express those two lines according to a common reference frame, the one of the left camera for instance. To reach it, we will try to express a geometric relation between both cameras.