Reference frames and changes of reference frames
The tridimensional space of the scene is fitted with its orthonormal reference frame
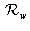. Each of the two cameras has its own orthonormal reference frame: we will call them left camera reference frame
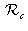and right camera reference frame
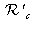. Figure 12 illustrates those three reference frames as well as the rigid transformations allowing the expression of a point in another reference frame.
![[zoom...]](javascript:window.open(%22../res/figure_12_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
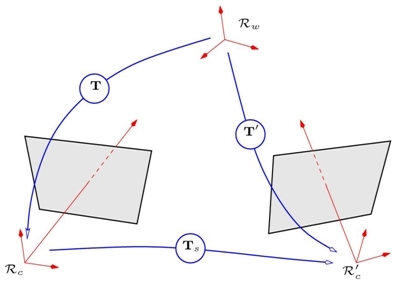
With those conventions, we can write the following relations down:
These equations show us that the three transformations are not independent since we can determine one of them by using the two others:
When a point
of the scene is simultaneously visible by both cameras, it gives us two points:
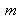for the left camera and
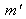for the right one. Using the geometric model of the camera and the relation of dependence between the three reference frames
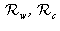and
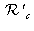, we can write the relations of
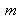and
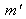according to M: