Le principe d'Huygens-Fresnel
Soit Σ une surface diffractante (voir figure II-1). Le principe d'Huygens Fresnel peut être exprimé par :
où
,
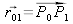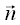est un vecteur unitaire
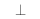à Σ ,
,
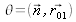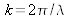, dS surface élémentaire entourant
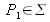, U(P1) et U(P0) amplitudes des champs en P1
et P0
.
![[zoom...]](javascript:window.open(%22../res/image_II_01_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
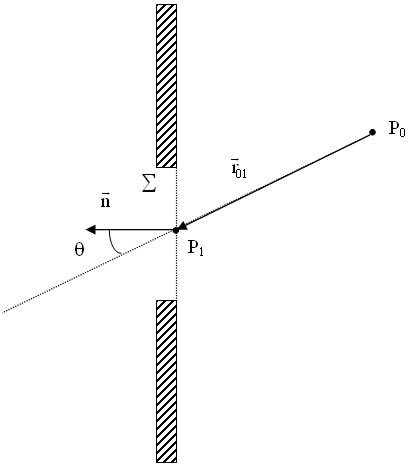
Signification physique de l'Eq. II-1 :
L'amplitude du champ au point P0 après l'ouverture est exprimé comme étent la superposition d'ondes sphériques divergentes
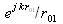émises par toutes les sources secondaires P1 qui constituent l'ouverture diffractante Σ.
La source secondaire située en P1 a les propriétés suivantes :
-
elle a une amplitude complexe proportionnelle à l'amplitude de l'onde incidente U(P1) .
-
elle est pondérée par un cosθ exprimant la directivité par rapport au point d'observation et pondérée par dS exprimant la surface élémentaire effective qui participe à l'émission
Il est important de remarquer ici que ce principe n'est rien d'autre en réalité qu'une intégrale de superposition exprimant la linéarité du système. C'est une infinité de sources secondaires sur Σ qui interférent en P0.
On peut écrire :
où h est une fonction de pondération définie par :