Signal d'interférences

Dans ce qui suit on considère que les deux ondes sont cohérentes temporellement, spatialement et en polarisation. Dans ce contexte, le signal observable s'écrit simplement :

On sous entend la dépendance spatiale avec par la suite à chaque fois que ce sera possible. Si on pose et 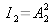, le signal d'interférences s'écrit aussi [3] :

avec :

où on note  la différence de chemin optique entre les deux ondes.

Le phénomène d'interférences se manifeste par une alternance de zones sombres pour lesquelles et de zones brillantes pour lesquelles . Notons 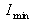le signal minimum et le signal maximum, nous avons :

On caractérise le contraste entre ces deux zones extrémales par le facteur de visibilité [3] :

Le contraste maximum est égal à 1 et il est obtenu pour , c'est à dire que les deux ondes ont même amplitude en tout point de l'espace. Si 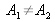, le contraste est inférieur à 1 et 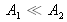si ou si , on a .

Les zones de maxima sont obtenues pour , soit

Les zones de minima sont obtenues pour , soit

Le terme  s'appelle la phase des interférences. Il est constitué de la différence des phases optiques des deux ondes et il est proportionnel à une différence de chemins optiques.

La distance, dans le plan d'observation, qui sépare deux zones consécutives de même nature est appelée interfrange.

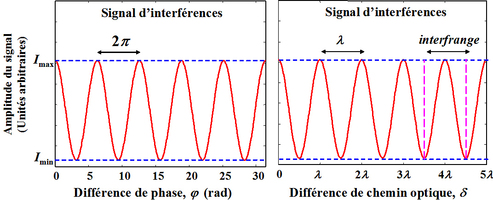
La figure 2 illustre les propriétés du signal d'interférences.

On s'intéresse maintenant à deux cas particuliers : les deux ondes sont planes et les deux ondes sont sphériques.