Cas de deux ondes sphériques

Considérons deux ondes sphériques co-polarisées (c'est à dire polarisées parallèlement) suivant x et se propageant vers les z positifs. La figure 5 illustre la géométrie du problème.

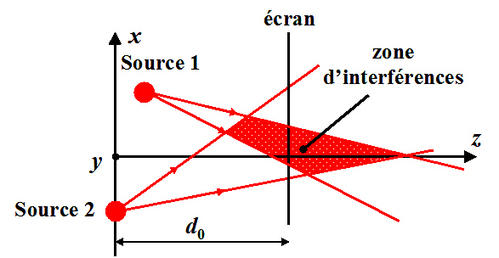
Dans ce cas, nous avons simplement :

pour la première onde et :

pour la seconde. Notons et les coordonnées des points sources des deux ondes sphériques. Nous avons en tout point de cordonnées :

La phase des interférences est , soit :

La figure 6 montre le champ spatial d'interférences dans la zone de superposition des deux ondes dans le plan (x, z) à gauche et dans le plan de coupe à droite (plan (x, y, z = d0)).

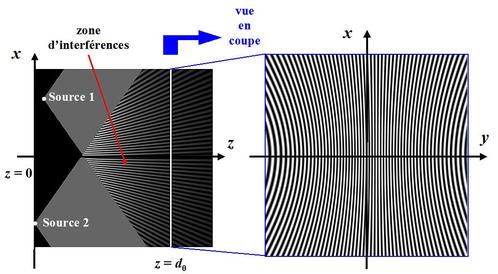
On constate que l'amplitude des interférences décroît avec la distance aux sources. Ceci est dû au terme en en facteur de chaque amplitude complexe. On pourra admettre que « loin des sources » ce terme est approximativement constant.

Dans l'espace (x, y, z), une frange brillante est localisée par la condition :

soit :

avec . Cette relation n'est pas d'une utilisation simple.

Cependant on peut expliciter l'interfrange dans le cas de l'approximation parabolique. Posons et . A la condition que l'approximation de Fresnel soit valable, une frange brillante est localisée par la condition :

ce qui donne :

avec :

Considérons un cas idéal : supposons que les sources soient placées symétriquement sur l'axe x de part et d'autre de l'origine en et avec et 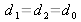et que la zone d'observation est placée à (figure 7).

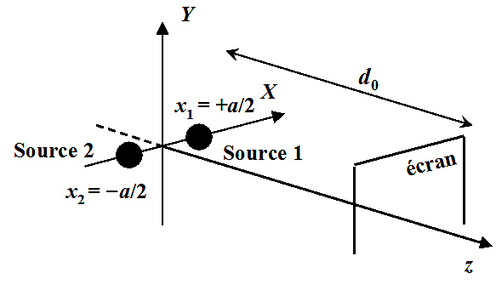
Dans ce cas, il vient simplement :

Avec cette configuration, les franges sont rectilignes et verticales parallèles à l'axe y. On peut observer sur la figure 6 que ce résultat correspond au centre de l'écran. La frange brillante d'ordre k est donc localisée en xk tel que :

et la frange brillante suivante, d'ordre k+1 est localisée en xk+1 tel que :

L'interfrange est donc :

Avec l'approximation parabolique, l'interfrange est constante suivant la direction x.