Cas de deux ondes planes

Considérons deux ondes planes se propageant vers les z positifs et de vecteurs d'ondes non colinéaires à z mais appartenant au plan {x,z}. La figure 3 illustre la géométrie du problème.

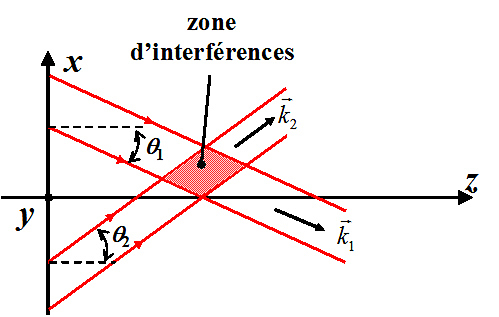
Dans ce cas, nous avons simplement :

pour la première onde et :

pour la seconde. Compte tenu que :

et que :

La figure 4 montre le champ spatial d'interférences dans la zone de superposition des deux ondes.

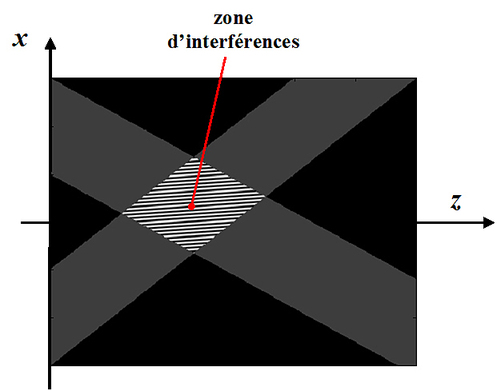
La distance qui sépare deux zones consécutives de même nature est l'interfrange. Pour z constant, l'abscisse x de la frange brillante d'ordre k quelconque est tel que :

Dans la direction x, pour la frange brillante consécutive à la précédente, la phase optique a varié de 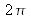et nous avons :

suivant la direction x, la distance qui sépare les deux franges brillantes (interfrange en x) est donc définie par :

où .

En raisonnant de la même façon dans la direction z, il vient l'interfrange en z :

où .

Dans le cas où il vient :

Les franges sont donc parallèles à l'axe z.

Pour fixer les ordres de grandeurs, considérons microns et , nous obtenons . L'interfrange est du même ordre de grandeur que la longueur d'onde. Le passage d'une frange brillante à une autre offre donc une sensibilité sub-micrométrique.