Choix d'un facteur d'élargissement

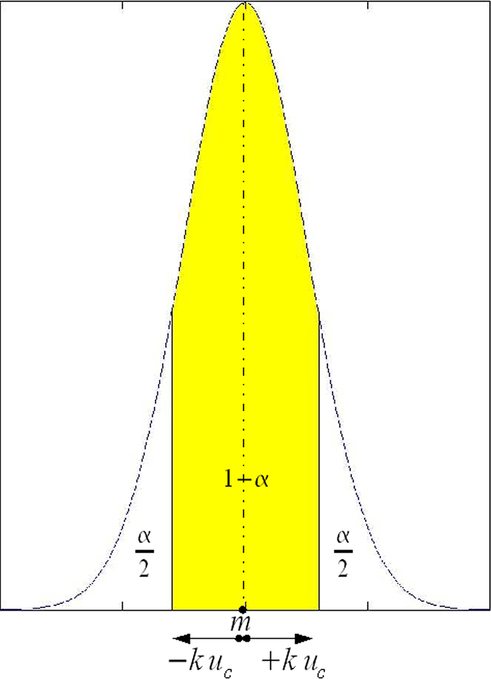
Si les résultats de mesure se répartissent suivant une loi normale autour de la valeur moyenne m (cf. figure 1), les valeurs respectives du facteur d'élargissement k et du niveau de confiance 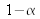sont rassemblées dans le tableau 3.

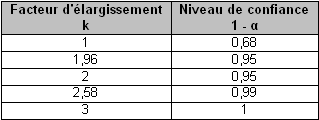
Ces valeurs ne sont rigoureusement valables que lorsque le nombre N de répétitions des mesures est important (typiquement N≥30). Dans la pratique, cela est rarement le cas, il faut alors utiliser la loi de t ou loi de Student que suit la variable 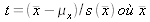est la moyenne arithmétique de N observations indépendantes xk de x et 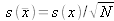l 'écart-type expérimental de la moyenne 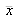. Il est à noter que la loi de Student n'est valide que si la variable aléatoire x suit une loi normale d'espérance mathématique µx et d'écart-type .

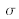En conséquence, si le mesurande Y est une grandeur unique X suivant une loi normale, telle que Y=X et si X est estimé par la moyenne 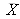arithmétique de N observations répétées indépendantes Xk de X, avec un écart-type expérimental de la moyenne 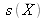, alors 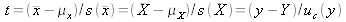est distribué selon la loi de student avec :

c'est à dire

ou encore

Dans ces expressions, 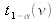est la valeur de t pour une valeur donnée du paramètre ν (nombre de degrés de liberté) telle que l'intervalle 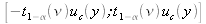est associé à un niveau de confiance 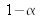. Autrement dit l'incertitude élargie est