Nombre de degrés de liberté

Le nombre de degrés de liberté ν est égal à 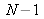dans le cas de la mesure directe d'une grandeur estimée par la moyenne arithmétique de N observations indépendantes. Si les N observations sont utilisées pour déterminer la pente 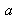et l'ordonnée à l'origine b d'une droite par la méthode des moindres carrés (cas d'une droite d'étalonnage telle que ), le nombre de degrés de liberté associé respectivement aux incertitudes-types et est . Pour un ajustement par méthode des moindres carrés de p paramètres pour N données, le nombre de degrés de liberté de l'incertitude-type de chaque paramètre est . Les différents cas énumérés ci-dessus sont rassemblés dans le tableau 4.

Une sélection de valeurs de 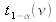pour différentes valeurs du niveau de confiance 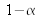et du nombre de degrés de liberté ν est donnée dans le tableau 5.

Lorsque ν → ∞, la loi de Student tend vers une loi normale et 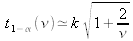où k est le facteur d'élargissement nécessaire pour obtenir un intervalle de confiance de niveau pour une variable distribuée normalement. Ainsi, dans le tableau 5 la valeur de 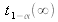pour un niveau de confiance donné 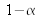est égale à la valeur de k pour la même valeur de 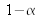dans le tableau 3. À partir de l'expression de 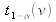, on peut aussi évaluer le nombre de degrés de liberté νL pour lequel 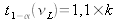permettant d'évaluer le nombre de mesures répétées 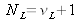au delà duquel la loi de Student est à moins de 10% d'une loi normale soit

d'où

soit

Ainsi, il faut à priori au moins 10 mesures répétées pour approcher à 10% près une loi normale décrivant la répartition des valeurs de la grandeur mesurée autour de sa valeur moyenne.

La loi de Student ne décrit pas en général la loi de la variable si u2 c (y) est la somme de plusieurs composantes de variance estimées 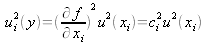même si chaque xi est l'estimation d'une grandeur d'entrée Xi normalement distribuée. Il est cependant possible d'utiliser la loi de Student avec un nombre effectif de degrés de liberté νeff obtenu par la formule de Welch-Satterthwaite ( , , )

où ν i est le nombre de degrés de liberté de chaque composante de l'incertitude-type composée uc(y) telle que . Pour une composante obtenue par une évaluation de Type A, ν i est associé au nombre d'observations répétées indépendantes de la grandeur d'entrée correspondante et au nombre de paramètres déterminés à partir de ces observations (cf. tableau 4). Pour une composante obtenue par une évaluation de Type B, ν i est évalué à partir de la fiabilité que l'on peut attacher à la valeur de cette composante suivant l'expression

où 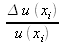est l'incertitude relative de u(xi). C'est une grandeur subjective dont la valeur s'obtient par un jugement scientifique fondé sur l'ensemble des informations disponibles. À noter que si u(xi) peut être considéré comme connu exactement alors νi→∞.