Photons X
La réduction de vitesse de propagation que subit une onde lumineuse arrivant du vide dans la matière peut s'expliquer avec des arguments simples: le champ électrique périodique de l'onde incidente exerce une force sur les électrons du milieu. Cette force entraîne l'oscillation des électrons à la même fréquence que l'onde incidente ce qui se traduit par l'émission d'une onde électromagnétique de même fréquence. Le champ total résultant est la superposition cohérente des champs de l'onde incidente et de l'onde émise par le milieu. L'interférence de ces ondes conduit à une propagation plus lente dans le milieu matériel que dans le vide. Le même raisonnement s'applique à la propagation des rayons-X dans la matière.
Les rayons-X interagissent avec les électrons de l'atome. L'indice de réfraction aux rayons-X d'un matériau s'obtient à partir du modèle phénoménologique classique de l'électron élastiquement lié. L'équation fondamentale de la dynamique appliquée à l'électron tient compte d'une force de Lorentz due au champ électromagnétique local induit par l'onde incidente, d'une force de rappel électron-noyau (de constante de rappel
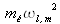) et d'un freinage de type visqueux de ses déplacements (de constante de friction
). La pulsation de l'électron m de l'atome l est notée
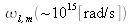et est infiniment plus faible que celle de l'onde électromagnétique incidente
. On suppose donc que l'électron va vibrer sous l'influence du champ incident à la pulsation forcée
. Ce modèle conduit à l'expression suivante pour l'indice de réfraction [] :
où mé est la masse d'un électron (9,109.10-31 kg) et e est sa charge (1,602.10-19 C).
Le facteur de
diffusion complexe
fl,m peut se décompose en la somme de trois termes pour l'atome l :
et
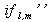qui sont accessibles dans la littérature pour chaque atome ou ion [
]. Ce sont respectivement le nombre total d'électrons, la partie réelle et la partie imaginaire du facteur de diffusion anomale. Seul le second et troisième terme dépendent de la longueur d'onde des rayons-X utilisés. En pratique, le nombre d'atomes par unité de volume s'obtient à partir de la densité massique
en atomes l et à partir de la masse atomique Al, avec l'expression :
, où Na est la constante d'Avogadro égale à 6,022 1023.
Pour un matériau uniquement constitué de l'élément chimique l on obtient pour les rayons-X :
où
et correspond au rayon classique de l'électron. Cette constante quantifie la force de l'interaction d'un électron avec un photon X.
Dans ces expressions,
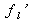apparaît comme une correction au nombre total d'électrons Zl de l'atome l dans l'expression de la densité électronique du matériau et
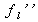introduit la présence de seuils d'absorption à des longueurs d'ondes particulières.
Ces deux corrections dépendent fortement de la longueur d'onde et peuvent être très importantes.