Neutrons et pseudo-potentiel de Fermi
Les neutrons interagissent principalement avec le noyau de l'atome. Dans le cadre de la théorie quantique, l'étude de la diffusion d'un neutron par un atome fixe passe par la recherche de la fonction d'onde
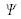solution de l'équation de Schrödinger. De manière analogue au traitement de la diffusion scalaire selon le formalisme optique présenté, la fonction d'onde
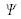est exprimée à partir de l'interférence d'une onde incidente
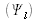et d'une onde diffusée
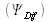. On pose alors les conditions suivantes :
où les fonctions d'onde se notent
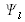pour l'onde plane incidente,
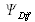pour l'onde diffusée supposée sphérique et
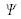pour la solution recherchée. H0 est l'Hamiltonien du système en l'absence d'interactions avec le neutron, E est l'énergie du système qui est conservée au cours de la diffusion et G est a fonction de Green dite retardée pour l'onde sphérique. La solution doit satisfaire l'équation de Lippmann-Schwinger qui passe par la détermination de l'opérateur de transition T (équation 2.1.5 de la référence []) :
Fermi en 1936 proposa l'expression suivante pour l'opérateur de transition :
où a est une longueur de diffusion égale au premier terme du développement de l'amplitude de diffusion
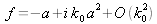et dont il est la limite basse énergies (équation 2.3.38 de la référence [], les différents termes de f sont définis après l'équation 2.2.27). Ce résultat a été étendu au cas des atomes liés, en supposant qu'à l'instant de la collision, les interactions interatomiques étaient négligeables. Cette hypothèse dite "Impulse approximation" est depuis justifiée puisque les forces interatomiques sont typiquement de l'ordre de 1eV sur une distance de 1Å, alors que le potentiel d'interaction neutron-noyau est estimé à près de 40.106 eV sur un rayon de quelques fm. Le pseudo-potentiel de Fermi permet de quantifier l'interaction neutron-noyau lié et a pour expression :
Dans cette expression on a substitué à la constante a de l'opérateur la constante bnoyau appelée longueur de diffusion liée. Ces constantes sont liées par la relation :
Cette substitution (de a par b) correspond au passage du référentiel attaché au centre de masse à celui attaché au laboratoire. Le mot lié ne se réfère pas à la liaison chimique et ces quantités sont toutes deux applicables aux gaz monoatomiques par exemple. L'expression de V est un pseudo-potentiel central de type cœur dur décrivant une interaction de très faible extension spatiale (
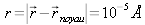) avec le neutron situé à la position
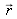. L'interaction est centrée sur la position du noyau
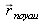telle un dirac
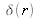et est répulsive (
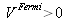) pour les valeurs positives de bnoyau . Cette grandeur phénoménologique se détermine expérimentalement et évalue, en quelques sortes, la force de l'interaction neutron-matière.
Pour les neutrons, nous avons introduit dans le cadre de la théorie élémentaire de la diffusion l'indice de réfraction du matériau par l'expression :
Un formalisme plus rigoureux que nous n'expliciterons pas ici en raison de sa complexité introduit des corrections au champ local []. Il est souvent possible de séparer en deux contributions l'indice optique tout en gardant une excellente précision. De même, la longueur de diffusion du noyau lié se sépare aussi en une partie réelle et une partie imaginaire conduisant à l'expression :
Pour expliciter l'origine de ces deux contributions, nous devons rappeler que les neutrons sont sensibles au magnétisme et ont un spin s=1/2 pouvant interagir avec les spins nucléaires I des atomes rencontrés. La longueur de diffusion liée devient donc dépendante de I et son expression la plus générale (invariante par rotation) est :
Lorsque les noyaux ou les neutrons ne sont pas polarisés, la moyenne au cours du temps et sur toutes les orientations possibles des vecteurs spin annule le second terme de cette somme. On obtient donc la longueur de diffusion Cohérente :
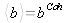. Par contre l'expression du carré des fluctuations de b conserve pour cette moyenne une partie dépendante des spins et s'exprime comme :
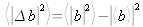, où
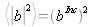. Les sections efficaces de diffusion dites cohérente et incohérente s'obtiennent à partir de ces grandeurs. Leur somme correspond à la section efficace totale de diffusion :
Un matériau constitué d'un élément chimique seul est généralement un mélange d'isotopes dont le spin est différent. Au désordre d'orientation des vecteurs spins s'ajoute alors un désordre isotopique. Une approche grossière de cette dépendance des sections efficaces en fonction des spins est de considérer qu'un neutron va sonder un matériau avec un potentiel d'interaction uniforme comme si ce milieu était constitué par un seul diffuseur effectif caractérisé par bCoch et qu'il existe des fluctuations aléatoires (temps et espace) de cette interaction donnant lieu à une diffusion isotrope dite incohérente et caractérisée par
.
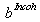Selon la théorie élémentaire de la diffusion, la section efficace d'absorption
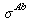vaut simplement
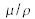. En réalité l'onde cohérente est aussi atténuée par la diffusion ce qui est pris en compte dans la théorie de la dispersion dite rigoureuse. On trouve dans la référence [] les sections efficaces d'absorption pour différents éléments calculées pour une longueur d'onde de
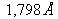. Le lien entre
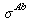et
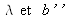est :
où la moyenne statistique s'effectue sur les spins des neutrons et des noyaux.
Pour illustrer cette discussion, considérons le cas de l'Hydrogène, 1H de spin ½.
Pour son isotope de masse double, le Deutérium, 2D de spin 1, les valeurs obtenues sont très différentes :
Ainsi la diffusion de H est pratiquement huit fois plus forte que celle de D mais est au contraire principalement incohérente. L'isotope D conduira donc pour une même structure moléculaire à un rapport signal cohérent sur bruit (incohérent) beaucoup plus avantageux que H et à une amplitude d'interaction cohérente beaucoup plus importante. Au sens défini ici, c'est elle qui permet d'atteindre l'information structurale. En réflectivité de neutrons la contribution incohérente est souvent assimilée à une source supplémentaire de bruit de fond.
On peut tenir compte de la perte d'intensité due à la diffusion incohérente d'un matériau en supposant que celle-ci se somme à l'intensité absorbée (neutrons capturés dans l'échantillon). Pour cela, on substitue à la section efficace d'absorption sa somme avec la section efficace de diffusion incohérente qui se trouve aussi dans la littérature. Pour le calcul on utilisera :
Ces termes se trouvent dans la littérature pour chaque isotope et pour la valeur moyenne obtenue à partir des abondances isotopiques naturelles des isotopes d'un élément. Cette moyenne inclue toutes celles qu'il convient d'effectuer pour des neutrons non polarisés dans le cadre de la diffusion élastique.