Introduction

Nous allons voir comment calculer l'indice de réfraction d'un matériau pour les rayons-X et pour les neutrons, ceci à partir de sa composition isotopique et en utilisant les données tabulées dans la littérature.

Il est pratique de décomposer l'indice de réfraction (n) d'un materiau en une composante réelle ( ) et une composante imaginaire ( ) :

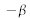Les composantes 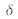et 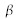caractérisent respectivement la diffusion et l'absorption d'un matériau à l'échelle macroscopique, c'est-à-dire lorsque les composantes du vecteur de diffusion 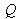sont grandes par rapport aux dimensions des mailles atomiques projetées dans l'espace réciproque. Ces valeurs dépendent de la nature et de la longueur d'onde du rayonnement utilisé. Elles s'obtiennent à partir de constantes accessibles dans la littérature ou sur internet. On peut par exemple utiliser la densité de longueur de diffusion 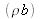et le coefficient linéaire d'absorption 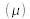du matériau avec les expressions :

L'expression de 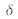n'est valide que lorsque est faible. C'est le cas généralement pour les neutrons et les rayons-X puisque les matériaux ont une densité de longueur de diffusion de l'ordre de , mais ce n'est pas le cas pour la lumière visible par exemple. Ainsi, le lien entre et respectivement et n'est pas aussi simple que l'indique cette relation (François de Bergevin en discute dans la référence []). Nous verrons qu'il est possible de lever cette approximation tout en conservant l'utilisation des valeurs calculées ou tabulées habituellement pour et 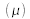. Ces deux constantes caractérisant un matériau sont particulièrement appréciées pour les raisons suivantes :

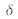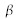• La densité de longueur de diffusion est indépendante de la longueur d'onde dans la gamme des énergies que nous considérons habituellement pour les rayons-X au laboratoire ou les faisceaux Neutrons (sauf dans le cas de l'utilisation de techniques très spécifiques bien au delà du cadre de ce cours). Lorsque les relations liant à et à ci-dessus sont valides et quand l'absorption du matériau est faible, la loi de Snell-Descartes relie à l'angle critique du matériau T par la relation simple :

• Le coefficient linéaire d'absorption a ici le même sens que celui utilisé dans la loi de Beer-Lambert pour la lumière visible. La transmission au travers d'une épaisseur x d'un matériau correspond au rapport du flux transmis par rapport au flux incident. Soit :

  Ainsi l'inverse de correspond à l'épaisseur traversée donnant une réduction de l'intensité du faisceau d'un facteur , soit . Cette grandeur s'appelle le parcours libre moyen sans absorption (en mètres).

Les valeurs de et de d'un matériau sont différentes pour la lumière, les rayons-X et pour les neutrons. On peut par contre comparer ces grandeurs entre elles ou ce qui permet entre autre de savoir si il vaut mieux utiliser le rayonnement X ou neutron pour étudier un échantillon donné. On recherche généralement le plus grand contraste entre couches successives (différence des ) ce qui se traduit par des franges d'interférences plus marquées dans le signal de R analysé. Des considérations expérimentales sont aussi a prendre en compte quant au choix de la technique et seront abordées dans un autre chapitre. Nous allons maintenant présenter leur calcul.