
Convolution sans déplacement par voie optique en incohérent
Plaçons deux transparences
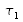 et
et
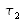 respectivement contre les lentilles L1
et L2
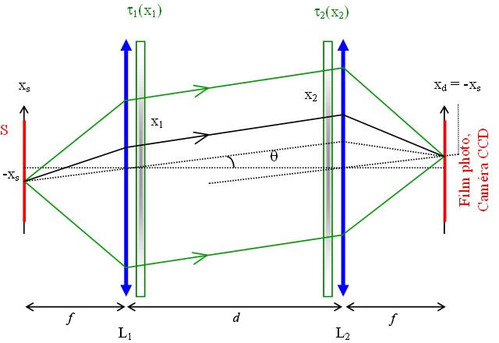
comme indiquée sur la figure II-7.
respectivement contre les lentilles L1
et L2
comme indiquée sur la figure II-7.
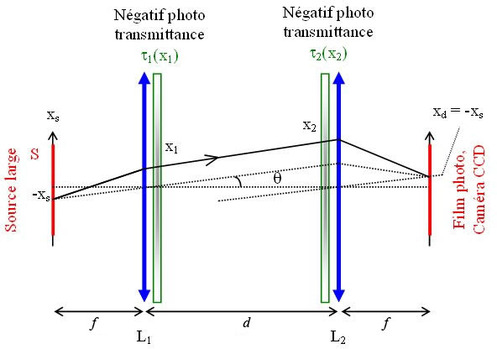
Soit un rayon provenant de S une source large situé à
 , il émerge de L1 en x1. La transmittance correspondante est
, il émerge de L1 en x1. La transmittance correspondante est
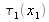 . Il arrive sur L2 en x2 pour converger en xd dans le plan du détecteur.
. Il arrive sur L2 en x2 pour converger en xd dans le plan du détecteur.
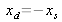 car les deux lentilles ont la même focale. L'intensité en ce point est :
car les deux lentilles ont la même focale. L'intensité en ce point est :
or
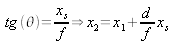 donc
donc
Soit

Si on considère l'ondelette sphérique issue du même point source en -xs, les rayons correspondant viennent tous se focaliser au même point -xd du détecteur qui fera la somme de toutes les intensités correspondant aux différents rayons (différents x) (voir figure II-8).
La généralisation sur deux dimensions est immédiate :
Nous avons réalisé l'opération convolution bidimensionnelle par voie optique. Cette opération est relativement longue à faire encore aujourd'hui par voie numérique. La rapidité de l'exécution de cette opération est surtout liée au parallélisme inhérent aux méthodes optiques qui effectuent le traitement sur tous les points du plan (x,y) en même temps. Il suffit d'un seul top horloge du détecteur matriciel pour voire l'image de la convolution
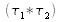 .
.