Synthèse d'un filtre passe bande en incohérent

Le spectre fréquentiel de l'intensité image s'écrit en incohérent (voir grain « Formation des images », partie: « Analyse fréquentielle des systèmes optiques formant des images):

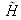est le spectre de l'objet, est la fonction de transfert cohérente avec :

Soient une pupille 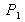ayant la forme des fentes d'Young et 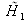la FTM du système comme indiquée sur la figure II-9.

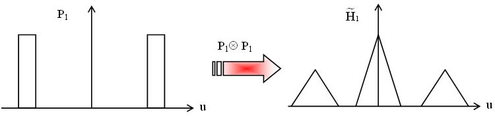
Supposons que l'on place une lame de phase de 180° 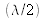sur l'une des fentes , la FTM du système devient suite à l'autocorrélation composée d'un triangle central positif et de deux triangles latéraux négatifs comme indiqué sur la figure II-10.

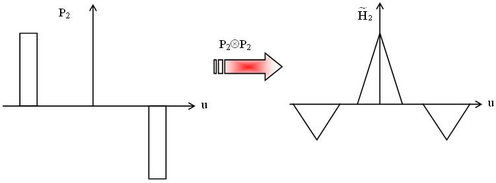
La soustraction de l'image obtenue par 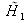de l'image obtenue par 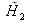donne :

On voit que pour cette FTM effective, (voir figure II-11) le fond continu et les basses fréquences spatiales ont disparu.

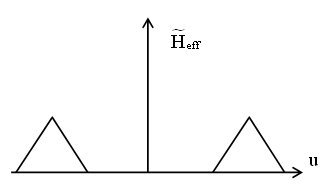
Cette FTM est une fonction de transfert passe bande. L'image obtenue ne contient que les fréquences spatiales les plus hautes, les applications possibles concernent la détection des contours.

La soustraction en optique incohérente par voie optique est impossible à faire (les intensités sont positives et s'ajoutent toujours). Il est par contre possible de transformer les images incohérentes en images cohérentes à l'aide d'un SLM et faire l'interférence de ces deux images en rajoutant un déphasage de à Ii2. Le résultat est une intensité représentant l'amplitude au carré de la différence. La synthèse d'autres FTM est possible pour plus de détails consultez la bibliographie [ ] .