
Le filtre de vander lugt (1963)
Introduction
Les filtres ainsi réalisés ont la propriété remarquable de permettre le contrôle efficace à la fois de l'amplitude et de la phase d'une fonction de transfert bien qu'ils ne soient formés que de figures purement absorbantes.
Réalisation de la fonction de transfert
Le masque fréquentiel (ou le filtre de Vander Lugt) est réalisé à l'aide d'un système interférométrique que l'on peut voir dans la figure II-15.
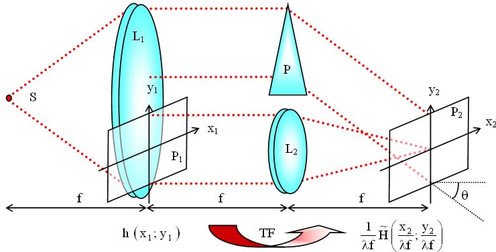
L'information codant la phase se trouve dans le terme d'interférence. L1 sert de collimateur. Une partie de cette lumière tombe sur le plan P1
dans lequel se trouve une transmittance en amplitude égale à la réponse impulsionnelle désirée h. La lentille L2 réalise la TF de h sur le film placé dans P2. L'autre partie de la lumière traverse le prisme P et arrive sur P2 sous incidence
 .
.
L'intensité incidente totale au niveau du film est déterminée par l'interférence de deux distributions d'amplitude (provenant de L2 et de P). L'onde plane inclinée est représentée par son amplitude complexe dans le plan P2 .
La distribution de l'intensité s'écrit donc :
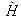 étant complexe, on peut poser dans le cas général :
étant complexe, on peut poser dans le cas général :
Ce qui donne pour l'intensité :
Cette forme montre comment le procédé interférométrique permet d'enregistrer une fonction complexe sur un détecteur sensible à l'intensité. L'information relative à l'amplitude et à la phase est enregistrée sous forme d'une modulation d'amplitude et de phase d'une onde porteuse de haute fréquence qui est introduite par l'onde de « référence » inclinée provenant du prisme. Pour réaliser le filtre, on développe le film de telle sorte que sa transmittance en amplitude soit proportionnelle à l'intensité d'exposition :
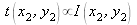
Dans le terme d'interférence (c.à.d. dans t) nous avons l'information requise pour réaliser le filtre de réponse impulsionnelle égale à h
Le problème qui reste est de montrer comment et sous quelles conditions on peut extraire cette information des autres termes présent dans I.
Traitement des données
Introduisons le masque
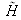 qu'on vient de réaliser dans le montage 4-f (dans le plan P2) (voir la figure II-16).
qu'on vient de réaliser dans le montage 4-f (dans le plan P2) (voir la figure II-16).
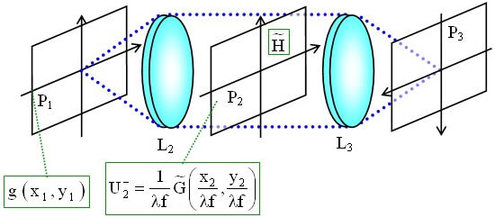
Soit g la fonction d'entrée que l'on souhaite filtrer.
L'amplitude U2
du champ transmis par le masque
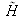 s'écrit
s'écrit
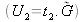 :
:
L3
réalise la TF de U2
dans P3 et sachant que
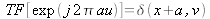 , l'amplitude du champ s'écrit :
, l'amplitude du champ s'écrit :
L2
divise l'amplitude du spectre par
 et réduit les coordonnées par
et réduit les coordonnées par
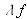 suivant chaque axe. L3 divise toujours l'amplitude du spectre par
suivant chaque axe. L3 divise toujours l'amplitude du spectre par
 mais remet cette fois-ci les coordonnées à la même échelle. Le théorème de similitude nous dit qu'il faut multiplier par
mais remet cette fois-ci les coordonnées à la même échelle. Le théorème de similitude nous dit qu'il faut multiplier par
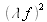 . Au total, le résultat revient à multiplier par
. Au total, le résultat revient à multiplier par
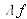 .
.
Sachant que
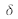 est l'élément neutre du produit de convolution avec lequel on effectue une translation suivant
est l'élément neutre du produit de convolution avec lequel on effectue une translation suivant
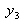 le troisième et quatrième terme deviennent:
le troisième et quatrième terme deviennent:
Les deux premiers termes centrés à l'origine n'ont pas d'intérêt particulier pour le filtrage. Dans P3
on observe trois régions où l'amplitude est différente de 0. Ces régions ne se recouvrent pas si
 est suffisamment grand devant l'étendue spatiale de h et de g (voir figure II-17).
est suffisamment grand devant l'étendue spatiale de h et de g (voir figure II-17).
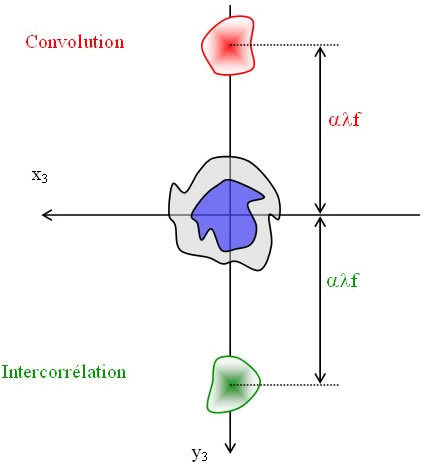
Ici l'avantage principal de ce filtre est de réaliser une fonction de transfert à valeurs complexes avec un filtre absorbant. La transmittance de phase dans le plan de Fourier est plus simple à réaliser techniquement (pas de contrôle de dimension, d'épaisseur ou d'indice).
Application à la reconnaissance des formes
Il s'agit de reconnaître l'emplacement d'une lettre (le P) présentée à l'entrée d'un système 4-f parmi différentes lettres (trois dans cet exemple).

On peut voir dans la figure II-18 l'image de la réponse impulsionnelle d'un filtre de Vander Lugt (à gauche) qui sera introduit dans le plan de filtrage. La réponse de ce filtre aux lettres Q, W et P (image de droite) à la sortie du système. A noter la présence du spot intense en dessous de P (au niveau du terme d'intercorrélation) indiquant un degré de ressemblance élevé entre cette lettre et le filtre choisi.
Il faut noter que l'inconvénient principal d'une telle méthode de reconnaissance utilisant la transformation de Fourier est sa grande sensibilité à la rotation et au changement d'échelle. D'autres transformées (telle que celle de Mellin) offre une sensibilité moindre au grandissement [ ].